7–1 CONDUCTANCE VS. RESISTANCE
It is well known that some materials, especially metals, permit electrical currents to easily flow through them. These materials, whose atomic structures readily provide free electrons, are referred to as good conductors.
Silver is the best of such conductors, but it is seldom used because of its high cost. Copper is almost as good a conductor as silver, is relatively inexpensive, and serves for most types of wiring. Aluminum, a fairly good conductor, is used where weight reduction is an important factor.
By contrast, other materials tend to prevent current from flowing through them. Such substances are known as nonconductors or insulators. Examples of insulators are glass, rubber, and nylon.
It is important to realize that not all materials can be so easily classified. The degree of conductivity varies over an extremely wide range. Conductors and insulators merely represent two extremes between which a great variety of materials are classified as poor conductors or semiconductors.
Among these poor conductors are metals and alloys that find use as resistance wire in heat-producing appliances such as electric ranges and heaters. Nickel-chromium, often called nichrome, is an example of such wire.
But even the extremes do not represent absolute perfection. Every conductor, no matter how good, still offers some resistance. Just how much resistance a conductor has de- pends on four factors, namely:
1. The type of material from which it is made
2. The conductor’s length
3. Its cross-sectional area (thickness)
4. Its temperature
These factors will be explored in the following sections.
7–2 RESISTIVITY OF MATERIALS
The resistance rating of different materials is based on a comparison of the number of ohms measured in a standard-sized sample of the material. In the metric sys- tem, for instance, the standard is a 1-centimeter cube whose resistance is measured in millionths of an ohm (microhms). Look at Figure A–1 in the Appendix, and com- pare the resistivity in microhm-centimeters. This resistivity is also known as specific resistance.
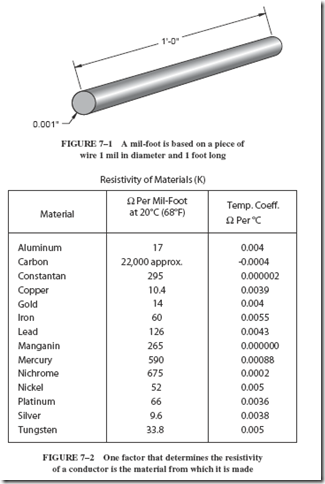
In the English system of measurement, the standard of resistivity is called the mil-foot. This standard is based on the resistance of a piece of wire 1 foot long with a diameter of 0.001 inch (1 mil 5 1/1,000). Figure 7–1 illustrates the concept of a mil-foot, and the chart in Figure 7–2 shows some characteristic values of resistivity.
7–3 LENGTH OF A CONDUCTOR
The resistance of any conductor is directly proportional to its length. For example, if 50 feet of wire has a resistance of 1 ohm, then 100 feet of the same wire will have a resistance of 2 ohms. In other words, the longer the wire, the more resistance it has. This simple fact must be taken into account whenever electricians plan the installation of a long supply line.
7–4 CROSS-SECTIONAL AREA (CSA) OF A CONDUCTOR IN CIRCULAR MILS
Resistance is inversely proportional to the cross-sectional area of the wire. This is a way of saying that the thicker the wire, the lower its resistance. A thick wire, as shown in Figure 7–3, allows many electrons to move through it easily, just as a wide road can carry many cars per hour or a large pipe can allow a large volume of water to flow through it.
Because the use of square inches or square feet results in complicated calculations and inconveniently small numbers for ordinary sizes of wire, a more convenient unit of area (thickness) is used. The circle in Figure 7–4 represents the end of a wire that is 1/1,000 of an inch thick. This distance, 0.001 inch, is 1 mil. The area of this circle, which is 1 mil in diameter, is 1 circular mil (CM). A circular mil is a unit of area (A) measurement. It is the same type of measurement as a square foot or an acre but more convenient to use.
For example, what is the area of a circle with a diameter of 0.002 inch? As Figure 7–5 illustrates, such a circle has an area exactly four times larger than a circle with a diameter of inch. If either the radius or the diameter of any flat surface is doubled, then the area will increase four times. Let us look at an example using the formula for finding the area of a circle, A 5 πr2. If the radius r of circle X is 5, then the area r2 is 25π. If the radius r of circle Y is 10 (double that of circle X), then the area of circle Y is 100π (four times that of circle X). There- fore, to answer the question about the area of a circle that has a diameter of 0.002 inch, we can say that the area is four times greater than that of a 1-mil circle, or 4 circular mils.
What is the area of a circle that has a diameter of 0.003 inch? Three-thousandths of an inch is 3 mils: 32 is 9. This circle is nine times as large in area as a 1-mil circle. The area of the circle, therefore, is 9 circular mils. The area of a circle, using circular mils, can be found by the following steps:
1. Write the diameter of the circle in mils.
2. Square this number (multiply it by itself); the result is the area of the circle in circular mils.
Note: 250,000 CM is also expressed as 250 Kcmil (formerly known as 250 MCM).
If the circular mils of a wire is known, it is a simple matter to reverse the mathematical procedure and find the diameter.
EXAMPLE 7–2
Given: A conductor with cross-sectional area of 100 circular mils.
Find: Its diameter in inches.
Solution
Not all conductors are circular in shape. Solid rectangular conductors (bus bars) are used to carry large currents. Bus bars are often easier to assemble and take up less space than the large-sized round conductors required to carry the same current. In addition, the flat shape of the bus bar provides more surface area from which heat can radiate.
The cross-sectional area of such a bus bar is figured in square mils rather than in circular mils. A square mil is defined as the area of a square with sides of 0.001 inch, as illustrated in Figure 7–6.
EXAMPLE 7–3
Given: A bus bar 4 inches wide and 0.25 inch thick, as shown in Figure 7–7.
Find: Its cross-sectional area in square mils.
Calculating the Resistance of a Wire
As previously stated, the resistance of a wire is a function of its resistivity (K); see Figure 7–2. Furthermore, it is directly proportional to its length (l) and inversely proportional to its cross-sectional area (A). This statement can be written mathematically as
Given: A two-wire power line is to be erected between poles 1,200 feet apart (the length of the wire is 2,400 feet). Resistance of the line should not be more than 1.7 ohms.
Find: The size of the aluminum wire to be used.
Solution
Labels: Direct current fundamentals