7–5 EFFECT OF TEMPERATURE ON RESISTANCE
Resistance depends not only on length, area, and kind of material, but also on the temperature of the material. Figure A–2 of the Appendix gives two sets of values for the resistance of copper at two different temperatures. (The resistance values given for the higher temperature are used when calculating motor and transformer windings since these windings are intended to operate warm.) These values in Figure A–2 show that as the temperature rises, the resistance of metals increases.
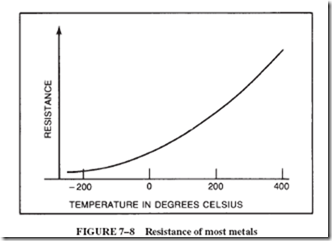
The graph in Figure 7–8 shows, in a general way, how the resistance of most metals increases as the temperature increases. Not only is the resistance greater, but it is also increasing at a faster rate as the temperature rises.
The resistance of carbon, however, decreases slightly with a rise in temperature. The resistance of conducting liquid solutions decreases rapidly with a temperature rise. Finally, the resistance of semiconductors, such as germanium and metal oxides, decreases very rapidly as the temperature goes up.
Not all metals increase in resistance at the same rate. The rate at normal temperatures is given as the temperature coefficient of resistance in Figure A–1 of the Appendix.
As the temperature approaches absolute 0 (–273°C), many metals and alloys lose all of their electrical resistance. This behavior is called superconductivity. When the niobium-alloy wire coils of extremely powerful electromagnets are cooled (by liquid helium) to temperatures about 4°C above absolute 0, the coils have a very low resistance. Thus, they can carry huge currents without an appreciable energy loss. Research scientists are developing super-cooled power lines that can be buried underground.
Using the Temperature Coefficient to Find Resistance at Higher Temperature
The resistance increase due to a higher temperature is equal to the original resistance multiplied by the temperature coefficient and by the rise in temperature in degrees. Ex- pressed in equation form, this statement becomes
Resistance increase 5 R x Coefficient x Degree rise
This resistance increase is added to the original resistance to give the resistance at the higher temperature.
EXAMPLE 7–7
Given: 10 feet of #30 platinum wire.
Find: The resistance of this wire if used in an oven at 500°F.
Solution
1. The resistance of 10 feet of #30 platinum wire at room temperature is found by comparison with copper: Figure A–2 (Appendix) gives the resistance of 1,000 feet of #30 copper wire as 103 ohms. Therefore, 10 feet of #30 copper wire has a resistance of 1.03 ohms. Platinum has 5.8 times as much resistance as copper. (This is derived from the Ohms Resistance per mil-foot column in Figure A–1 of the Appendix.) Therefore, 10 feet of platinum, at room temperature, has a resistance of
1.03 x 5.80 = 5.97 or 6 V
Thus, the original resistance in the formula for finding the amount of resistance increase is the value of 6 ohms at 68°F.
2. The temperature coefficient given in Figure A–1 (Appendix) is 0.003 per degree Celsius.
3. The rise of temperature in degrees must be found and expressed in degrees Celsius.
From 68°F to 500°F, there is a difference of 432°F. Since 1.8°F equals 1°C, we divide the 432°F temperature rise by 1.8 to establish that a change of 432°F is equivalent to a change of 240°C.
4. The three quantities needed to calculate the amount of change in resistance are now known. Thus, resistance increase is
6 V x 0.003 x 240°C = 4.3 V
This value is added to the original resistance of 6 ohms. As a result, the resistance of 10 feet of #30 platinum wire at 500°F is 6 ohms 1 4.3 ohms, or 10.3 ohms.
7–6 THE AMERICAN WIRE GAUGE (AWG)
It would be impractical having to calculate resistance for any given length and wire diameter. Such information is more readily available from the American Wire Gauge (AWG), also known as the Brown & Sharpe (B&S) Gauge.
The AWG was standardized in 1857 and is used mainly in the United States for measuring the diameters of round, solid, nonferrous electrical wire. The gauge size is important for determining the current carrying capacity of a conductor. Gauge sizes are determined by the number of draws necessary to produce a given diameter or wire. Electrical wire is produced by drawing it through a succession of dies, Figure 7–9.
Each time a wire passes through a die it is wrapped around a draw block several times. The draw block provides the pulling force necessary to draw the wire through the die. A 24 AWG wire would be drawn through 24 dies each having a smaller diameter. In the field, wire size can be determined with a wire gauge, Figure 7–10.
One side of the wire gauge lists the AWG size of the wire, Figure 7–11. The opposite side of the wire gauge indicates the diameter of the wire in thousandths of an inch, Figure 7–12. When determining wire size, first remove the insulation from around the conductor. The slots in the wire gauge, not the holes behind the slots, are used to determine the size, Figure 7–13.
The AWG assigns numbers from 0 to 44; see Figure A–2 of the Appendix. The table is self-explanatory, but the following observations may be useful:
• The larger the number, the smaller the wire.
• A #2 wire is nearly the size of a standard wooden pencil.
• A #44 wire is about the thickness of a fine hair.
• Wires larger than 0-gauge are labeled 00 (2/0), 000 (3/0), and 0000 (4/0), respectively.
• Wires larger than 0000 (4/0) are classified by cross-sectional area in CM, the next larger size being 250,000 CM 5 250 Kcmil (see Example 7–1).
• Odd-numbered conductors are rarely used and seldom stocked by wholesalers.
• The most prevalent wire sizes used in house wiring are #14 and #12.
• A #14-gauge wire is the smallest wire permissible by the National Electric Code® to be used for permanent installations.
• No. 8-gauge wire can be used for installing electric kitchen ranges and other heavy-duty appliances.
• No. 22-gauge wire may be used for electronic circuits.
• Ordinary lamp cords are generally made of #16 or #18 wire.
• A stranded wire has the same amount of copper and the same current-carrying capacity as a solid wire of the same size.
7–7 STRANDED WIRE AND CABLE
Bunch Stranding
Bunch-stranded wire is a collection of wires twisted together. These wires are not placed in specific geometrical arrangement. For example, #18 lamp cord contains 16 #30 wires that are loosely twisted together in the same direction.
Concentric Stranding
For this type of wire stranding, a center wire is surrounded by one or more definite layers of wires. Each wire layer contains six wires more than the layer immediately beneath it, Figures 7–14 and 7–15. When several wire layers are used, each layer is twisted in a direction opposite to that of the layer under it.
The diameter of the wire strands used in a cable depends on the flexibility required. Obviously, a cable made up of many fine wire strands is a lot more flexible than an equally sized cable constructed from only a few thick strands. However, since even fine wire will break if bent back and forth many times, stiffer wire may be used in addition to copper wire to increase the durability of a cable. One type of #25 microphone cable consists of four strands of #33 copperweld wire added to three strands of #33 copper wire. Steel as well as copperweld wire may be used to supply extra strength to large cables.
Rope Stranding
A rope-stranded cable consists of several concentric cables twisted together. The 7 x 19 rope-stranded cable shown in Figure 7–16 consists of seven 19-strand conductors twisted together.
Cables larger than #4/0 are rated in circular mils. Standard sizes range from 200 Kcmil to 5,000 Kcmil. These cables may be covered with any of a great variety of insulation materials.
Cables are not always circular. Flat braid is available in many shapes and sizes. The battery grounding strap on an automobile used to be made from wire in the form of a flat braid.
Labels: Direct current fundamentals