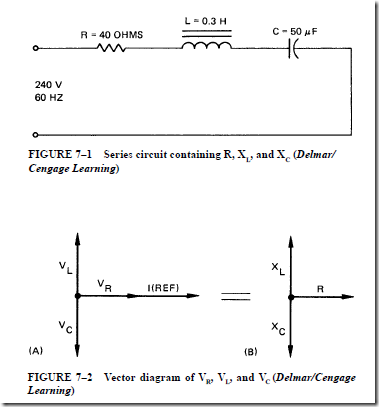
Figure 7–1 shows a series circuit containing a resistor, an inductance coil with negligible resistance, and a capacitor. For this type of circuit, it is important to remember that
(1) the voltage (V) across an inductor (L) leads the current (I), and (2) the current (I) in a capacitor (C) leads the voltage (V).
This information can be expressed by means of a vector diagram, as in Figure 7–2.
The voltage component across the inductor (V ) is rotated counterclockwise so that it leads the current (I) by 90°. The current in the capacitor leads the voltage (VC) by 90°. The diagram shows that the voltage drops across the inductor and the capacitor are 180° out of phase (Figure 7–2A). This means that they oppose each other. When the components in the voltage vector diagram are divided by I, the resulting reactance vectors also oppose each other (Figure 7–2B).
Net Reactance of an RLC Series Circuit
The net reactance, in ohms, for an RLC series circuit is found by subtracting the capacitive reactance from the inductive reactance. For the circuit in Figure 7–1:
This example shows that 53.1 n of inductive reactance is canceled by the 53.1 n of capacitive reactance. The difference of 60 n represents the inductive reactance that affects the operation of the series circuit.
Impedance of the RLC Series Circuit
Impedance is the result of the combination of resistance and reactance. In Figure 7–1, the impedance is the combination of the resistance of 40 n and the difference between the inductive reactance and the capacitive reactance. The impedance for this circuit is
Voltage Drop across the Elements
The voltage drops across the resistor, the inductor coil, and the capacitor are deter- mined as follows:
Voltage drop across R:
Voltage drop across C:
Vector Diagram of the Series RLC Circuit
The vector diagram for the series RLC circuit of Figure 7–1 is shown in Figure 7–3. V is shown in the positive Y direction, and V is shown in the negative Y direction. The magnitude of V – VC is found by means of the vector addition rule of placing vectors head to tail. Thus, the V vector is placed on top of the V vector (head to tail) to find the difference: V – VC = 200 V. It is important that the student understand that the vectors were not subtracted to equal 200 V, but were added.
The vector sum of the voltage across the resistor, 133.2 V, and the voltage across the net inductive reactance, 200 V, is equal to the line voltage, 240 V:
Power Factor of the Series RLC Circuit
The power factor of this type of circuit can be determined by any of the methods used in previous series circuit problems. The power factor of this circuit is
Because the inductive reactance is greater than the capacitive reactance, this series circuit has a lagging power factor. The power factor has a lagging phase angle of 56.3°. This means that the current lags the line voltage by 56.3°, as shown in Figure 7–3.
PROBLEM 1
Statement of the Problem
For the circuit in Figure 7–1, the inductive reactance is greater than the capacitive reactance. For the circuit in Figure 7–4, the capacitive reactance is more than the inductive reactance.
This series circuit consists of three components: a noninductive 20-n resistor, an inductance coil having an inductance of 0.1 H and negligible resistance, and a 50-µF
capacitor. These components are connected to a 120-V, 60-Hz source. Figure 7–4 also shows the relationship between the line current and voltage waveforms across each component. The voltage across the resistance is in phase with the current, the voltage across the inductor coil leads the current by 90°, and the voltage across the capacitor lags the current by 90°.
The following circuit values are to be determined for this series RLC circuit:
1. The impedance
2. The current
3. The voltage across (a) the resistor, (b) the coil, and (c) the capacitor
4. The line voltage (check)
5. The true power, in watts, taken by the series circuit
6. The magnetizing VARs required by the coil
7. The magnetizing VARs supplied by the capacitor
8. The net magnetizing VARs supplied to the power source
9. The input volt-amperes for the series circuit
10. The circuit power factor and the phase angle
Solution
1. The inductive reactance equals 21TfL, and the capacitive reactance equals
Therefore, the impedance formula can be stated in either of these forms:
If the capacitive reactance is greater than the inductive reactance, the quantity in parentheses in the formulas is negative. Because the square of a negative number is
4. The voltage across the capacitor is greater than the voltage across the coil. These two voltages are 180° out of phase and oppose each other. Subtracting these voltages yields
252.52 - 179.45 = 73.07 V
This means that the part of the capacitor voltage that is not canceled by the coil volt- age is equal to 73 V. The vectorial addition of 73 V and the loss across the resistor,
95.2 V, gives the line voltage, or 120 V. The line voltage can be determined using the right-triangle method, in which
5. The true power, in watts, taken by the series circuit can be determined by
8. The net magnetizing VARs supplied to the source is the difference between the VARs supplied by the capacitor and the VARs required by the coil: 1202 - 854 = 348 VARs. The net magnetizing VARs can also be calculated using the net reactance
(15.35 n capacitive) and the net reactive voltage (73.07 V):
10. There are three methods of calculating the power factor of the series circuit:
The capacitive reactance is greater than the inductive reactance of this circuit. This means that all of the inductive reactance is canceled. The circuit power factor and the phase angle are determined by the resistance and the capacitive reactance that is not canceled by the inductive reactance. As a result, the series circuit has a leading power factor. The current leads the line voltage by a phase angle of 37.5°.
Voltage and Current Vector Diagram
A voltage and current vector diagram is shown in Figure 7–5 for the series circuit of Figure 7–4. The two reactance voltages are 180 electrical degrees out of phase. Because the voltage across the capacitor is larger, the voltage across the coil is subtracted from V . The difference of V – VL is combined by vector addition with the voltage across the resistor to give the line voltage. The current leads the line voltage in a counterclockwise direction by 37.5°.
Labels: Alternating current fundamentals