Series–Parallel Circuits : Admittance, conductance, and susceptance

Series–Parallel Circuits

ADMITTANCE, CONDUCTANCE, AND SUSCEPTANCE Admittance

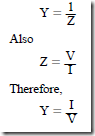
Impedance is the measurement of the opposition to electron flow in a circuit containing resistance and reactance. The unit of admittance is a measurement of the ease of electron flow through a circuit or component containing resistance and reactance. This means that admittance is the inverse, or reciprocal, of impedance. The unit of measurement for admittance is the siemens (abbreviated as S). (Formerly the unit of admittance was known as the mho, .) Admittance is indicated by the letter Y.

The relationship between admittance, in siemens, and the impedance, in ohms, is

Conductance

Conductance is a measurement of the ease of electron flow through a resistance. Conductance, like admittance, is measured in siemens. For dc circuits and ac circuits containing only noninductive resistance, the conductance is the reciprocal of the resistance. For ac circuits containing resistance and reactance, the conductance (G) is equal to the resistance divided by the square of the impedance:

G = R ÷ Z²

Susceptance

Susceptance measures the ease of electron flow through the reactance of an ac circuit. Like admittance and conductance, the unit of susceptance is the siemens. Susceptance (B) is equal to the reactance, in ohms, divided by the square of the impedance:

B = X ÷ Z²

Susceptances (B) in parallel and conductances (G) in parallel are added.

Relationship between Admittance, Conductance, and Susceptance The relationship between the admittance, the conductance, and the susceptance is the same as the relationship between the impedance, the resistance, and the reactance, as shown in Figure 9–1.

The admittance triangle in Figure 9–1 shows that the admittance (Y) is the hypotenuse of a right triangle:

PROBLEM 1

Statement of the Problem

The schematic diagram of a series–parallel circuit is shown in Figure 9–2. The series part of the circuit contains resistance and inductive reactance. The GBY method is to be used to find the following circuit values:

1. The total impedance, in ohms

2. The current for the series–parallel circuit

3. The power factor of the series–parallel circuit

Solution

1. This problem is solved by considering the circuit in sections. The values of the various quantities for sections A–B and C–D of the circuit in Figure 9–2 are shown in this table. The values in each circuit section connected in parallel are placed in the table as a convenient reference.

In the series part of the circuit between F and G, the resistance is 4 W and X is 9 W. For  the entire circuit, the resistance of the parallel section (E–F) is added to the resistance of the series portion (F–G):

PROBLEM 2

Statement of the Problem

In the series–parallel circuit shown in Figure 9–3, both the parallel and the series sections contain resistance and reactance.

The GBY method is to be used to determine the following values for this circuit:

1. The total impedance, in ohms

2. The current indicated by the ammeter

3. The power factor of the series–parallel circuit

Solution
1. The following table lists the given values for the parallel branches (A–B and C–D) of the circuit.

SUMMARY
• The GBY method of solving ac network circuits is commonly used because only basic mathematical processes are needed.
1. G = conductance. This unit is a measurement of the ease of electron flow through a circuit or component containing resistance.
a. It is measured in siemens.
b. It is the inverse or reciprocal of resistance in a dc circuit or an ac circuit containing only noninductive resistance:

2. B = susceptance. This unit is a measurement of the ease of electron flow through the reactance of an ac circuit.
a. It is measured in siemens.
b. It is expressed as the ratio of the reactance and the impedance squared:

3. Y = admittance. This unit is a measurement of the ease of electron flow through a circuit or component containing resistance and reactance (impedance).
a. It is measured in siemens.
b. It is the inverse or reciprocal of impedance.
c. The relationship between admittance, in siemens, and the impedance, in ohms, is

• The relationship between the admittance, the conductance, and the susceptance is the
same as the relationship between impedance, resistance, and reactance.
• The admittance (Y) is the hypotenuse of a right triangle:

• To determine the total susceptance, in siemens, for parallel branches in an ac circuit, the susceptance of the capacitor branch must be subtracted from the susceptance values of the other two branches.
1. The inductive reactance (XL) and the capacitive reactance (XC) cause opposite effects in an ac circuit.
2. The reciprocal values of XL and XC, expressed as susceptance, in siemens, also have opposite effects.
• The total admittance, in siemens, for a parallel circuit with a number of branches is

• The combined resistance for an ac circuit containing series and parallel branches is the sum of the resistance in the series branches and the resistance in the parallel branches, where the resistance in the parallel branches is

• The combined reactance (XL) for a circuit with series and parallel branches is the sum of the reactance in the series branches and the reactance in the parallel branches, where the reactance in the parallel branches is

Achievement Review
1. Explain the meaning of the following terms:
a. Admittance
b. Conductance
c. Susceptance
2. In the series–parallel circuit shown in Figure 9 –4, determine
a. the admittance, in siemens, of the parallel section of the circuit between points E and F.
b. the total impedance of the series–parallel circuit.

3. Using the circuit given in question 2, determine
a. the reading of the ammeter.
b. the current in amperes in the A–B circuit branch.
c. the power factor of the entire series–parallel circuit.
d. the total power, in watts, taken by the entire series–parallel circuit.
4. In the series–parallel circuit shown in Figure 9–5, determine
a. the admittance, in siemens, of the three branches connected in parallel.
b. the impedance, in ohms, of the entire series–parallel circuit.

Labels: Alternating current fundamentals