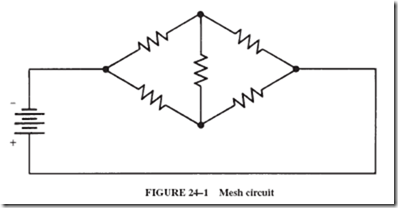
This method applies to circuits with a series of interconnected branches forming loops. Such circuits are also known as mesh circuits. The circuit in Figure 24–1 is an example of this.
The solution of such circuits requires the following procedure:
1. Identify all the loops in the circuit and identify corresponding loop currents, such as I1, I2, and I3.
2. Assign each current in an arbitrary direction.
3. For each loop, write an equation using Kirchhoff’s voltage law.
Note: If a resistor is part of two loops, it will have two different currents flowing in it that may be adding or subtracting each other.
4. Simplify the loop equations by substituting values and by collecting terms.
5. Solve the simultaneous equations for their unknown loop currents.
EXAMPLE 24–1
Given: A Wheatstone bridge circuit as shown in Figure 24–2. (Note: Wheatstone bridge circuits are covered in Chapter 17.)
Find: The amount and direction of all branch currents.
EXAMPLE 24–2
Given: The circuit shown in Figure 24–4.
Find: All the branch currents, using the loop method.
Solution
All components in this circuit are contained within two loops; therefore, this problem can be solved by using two loop currents only.
We suggest that you prove the results to yourself by computing the voltage drops and inserting the answers, with their respective polarities, into the drawing of Figure 24–4. Then use Kirchhoff’s voltage law to confirm your results.
24–2 THE SUPERPOSITION THEOREM
In a circuit with multiple power sources, each power source contributes toward the current flow through the resistors. The superposition theorem is developed on the principle that we can determine just how much each power source contributes toward the branch currents. We do this by considering only one power source at a time. For this purpose, the remaining power sources are replaced with a short-circuiting conductor. (To simplify our explanation, we assume that the internal resistance of the power source 5 0.)
We do this analysis for each power source, one at a time, and the resulting currents are then algebraically combined to determine the magnitude and direction of each current flow. This can be visualized by superpositioning the results in the original schematic diagram.
The following example will illustrate the procedure.
EXAMPLE 24–3
Given: The circuit shown in Figure 24–5.
Find: The magnitude and direction of all the current flowing through the resistors.
Solution
1. Omit the 36-volt power source by replacing it with a short circuit.
RT 5 4.5 ohms. Thus, the battery delivers 4 amperes, distributed as shown in Figure 24–6.
2. Omit the 18-volt battery by replacing it with a short circuit.
RT 5 7.2 ohms. Thus, the battery delivers 5 amperes, distributed as shown in Figure 24–7.
3. Superposition your results in the original drawing, as shown in Figure 24–8.
Inspection of these results will suggest the remainder of the solution. The currents through each resistor must be added algebraically. In other words, currents flowing in the same direction are being added, and currents flowing in opposite directions are being subtracted. The final results are shown in Figure 24–9.
EXAMPLE 24–4
Given: The circuit shown in Figure 24–10.
Find: The magnitude and direction of all branch currents, using the superposition theorem.
Solution
1. Eliminate the 6-volt and 2-volt batteries by replacing them with a short circuit.
RT = 4.133 ohms. Thus, the battery delivers 5.81 amperes, distributed as shown in Figure 24–11.
2. Omit the 24-volt and the 2-volt batteries and find the current due to the 6-volt power source only, as shown in Figure 24–12. Redraw the circuit to help you solve for RT and the branch currents. RT 5 5.166 ohms, and the current distribution is shown in Figure 24–13.
3. Next, determine the branch currents when only the 2-volt source is in the circuit, Figure 24–14. RT 5 3.647 ohms. Thus, the current distribution is as shown in Figure 24–14.
4. The results of the three preceding steps are now incorporated into the original circuit drawing, as shown in Figure 24–15. We can now algebraically combine these results to find the net current through each resistor. The final results are graphically presented in Figure 24–16.
Note: In case you have not noticed, this is the identical circuit we solved before by the loop current method in Example 24–2.
24–3 THEVENIN’S THEOREM
Occasionally, the electronics technician is confronted with a complex network of emfs and resistors for the purpose of verifying the electrical data for only one of the resistors. For example, let us consider the network shown in Figure 24–17 and assume that we need to know specific information about the resistor called RL. According to Thevenin’s theorem, we can simplify our task by reducing the rest of the network to a single equivalent series circuit of one emf and one resistance, known as Thevenin’s volt- age ETH and Thevenin’s resistance RTH.
In other words, we can pretend to place all components, except RL, into a black box and bring out only the two terminals labeled A and B. The contents within the black box may then be the venized, that is, reduced to the simple equivalent circuit as shown in Figure 24–18. The following example is designed to show how this can be done.
EXAMPLE 24–5
Given: The circuit shown in Figure 24–17.
Find: The magnitude and direction of the current through RL.
Solution
1. We the venize the circuit by the black box principle, and determine the voltage at points A and B, which is The venin’s voltage ETH. This can be done in the following manner:
a. Rearrange the circuit without RL, as shown in Figure 24–19.
b. Then, if the circuit actually exists, measure the voltage with a high-impedance
voltmeter, or
c. calculate the voltage drop by Kirchhoff’s voltage law, as follows: The two voltage sources have subtractive polarity and furnish a combined voltage of 18 volts to the loop containing 9 ohms. This results in a 2-ampere loop current with the resultant voltage drops as shown in Figure 24–19. Consequently, ETH 5 36 2 12 or (18 1 6) 5 24 volts.
2. Next, determine the resistance within the black box. This is known as Thevenin’s resistance, RTH. To do this, first replace the voltage sources with their internal
resistance. If the voltage sources are considered to be ideal (their internal resistance equals 0), simply replace them with a short circuit, as shown in Figure 24–20. Now we have two choices.
a. If the circuit actually exists, apply an ohmmeter at points A and B.
b. Otherwise, calculate the resistance within the black box. In this case
3. The results from steps 1 and 2 can now be used to show us the equivalent circuit within the black box, Figure 24–21.
When we apply the load resistor (RTH 5 2 Ω) to terminals A and B, it should become obvious that a current of 6 amperes is flowing from point B to point A. Compare this answer with that of Figure 24–9.
Let us reinforce what we have learned by the venizing one more circuit.
EXAMPLE 24–6
Given: The circuit shown in Figure 24–22.
Find: The magnitude and direction of the current through RL by thevenizing the network.
Solution
1. Rearranging the network within the black box yields the circuit conditions shown in Figure 24–23.
The loop current is
Therefore, the voltage drop across the 4-ohm resistor is equal to 10.588 volts. Hence, the voltage from A to B, Thevenin’s voltage, equals
2. Short-circuiting the voltage sources to find RTH, we obtain the following arrangement, Figure 24–24.
3. The Thevenin equivalent circuit (in the black box) is shown in Figure 24–25. The current through RL can now be computed as follows:
The direction of the current is from A to B.
Note: In case you did not notice, this is the identical circuit we have solved twice before, first by the loop current method in Example 24–2 and, second, by use of the superposition theorem in Example 24–4.
Labels: Direct current fundamentals