24–4 NORTON’S THEOREM
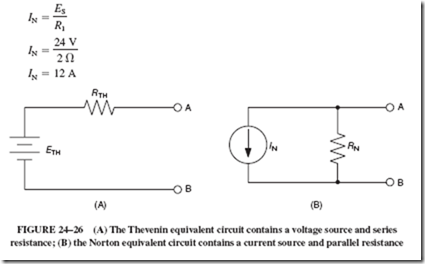
Norton’s theorem, developed by American scientist E. L. Norton, is used to reduce a circuit network into a simple current source and a single parallel resistor. This is the opposite of Thevenin’s theorem, which reduces a circuit network into a simple voltage source and a single series resistor; see Figure 24–26. Norton’s theorem assumes that the source of current is divided among parallel branches. A source current is often easier to work with—especially when calculating values for parallel circuits—than a voltage source, which drops voltages across series elements.
Current Sources
Power sources can be represented either as a voltage source or a current source. Voltage sources are generally shown as a battery with a resistance connected in series with the circuit to represent the internal resistance of the source. This is the case when using Thevenin’s theorem. Voltages sources are rated with some amount of voltage, such as 12 volts, 24 volts, and so on.
Power sources represented by a current source are connected to a parallel resistance that delivers a certain amount of current such as 1 ampere, 2 amperes, 3 amperes, and so on. Assume that a current source is rated at 1.5 amperes; see Figure 24–27. This means that 1.5 amperes will flow from the power source regardless of the circuit connected. In the circuit shown in Figure 24–27, 1.5 amperes flows through resistor RN.
A circuit similar to that used to illustrate Thevenin’s theorem can be used to illustrate Norton’s theorem; see Figure 24–28. In this basic circuit, a 2-ohm and a 6-ohm resistor are connected in series with a 24-volt power source. To determine the Norton equivalent of this circuit, imagine a short circuit placed across terminals A and B, as shown in Figure 24–29. Since the short circuit is placed directly across resistor R2, that resistance is effectively eliminated from the circuit and a resistance of 2 ohms is left connected in series with the voltage source. The next step is to determine the amount of current, IN, that can flow through the circuit.
Thus 12 amperes is the amount of current available in the Norton equivalent circuit.
The next step is to find the equivalent parallel resistance, RN, connected across the current source. To do this, remove the short circuit across terminals A and B. Now replace the power source with a short circuit (just as was done in determining the Thevenin equivalent circuit), as shown in Figure 24–30. The circuit now has a 2-ohm and a 6-ohm
The Norton equivalent circuit shown in Figure 24–31 is a 1.5-ohm resistor connected in parallel with a 12-ampere current source.
Now that the Norton equivalent for the circuit has been computed, any value of resistance can be connected across terminals A and B and the electrical values computed quickly. Assume that a 6-ohm resistor, RL, is connected across terminals A and B, as shown in Figure 24–32. The 6-ohm load resistor is connected in parallel with the Norton equivalent resistance of 1.5 ohms. This produces a total resistance of 1.2 ohms for the circuit. In the Norton equivalent circuit it is assumed that the Norton equivalent current, IN, flows at all times. In Figure 24–32, the Norton equivalent current is 12 amperes. Therefore, a current of 12 amperes flows through the 1.2-ohm resistance. This produces a voltage drop of 14.4 volts across the resistance (E 5 12 A 3 1.2 Ω). Since the resistors shown in Figure 24–32 are connected in parallel, 14.4 volts is dropped across each. This produces a current flow of 9.6 amperes through RN (14.4 V/1.5 Ω 5 9.6 A) and a current flow of 2.4 amperes through RL (14.4 V/6 Ω 5 2.4 A).
SUMMARY
Four different methods of analyzing complex mesh circuits have been discussed:
1. The loop current method, involving Kirchhoff’s law and the solution of simultaneous equations
2. The superposition theorem
3. Thevenin’s theorem
4. Norton’s theorem
The Loop Current Method
1. Label all terminal points with letters to identify the various paths.
2. Indicate the fixed polarity of all emf sources.
3. Assign a current to each branch of the network. An arbitrary direction may be given to each current.
4. Show the polarity of the voltage developed across each resistor as determined by the direction of the assumed currents.
5. Apply Kirchhoff’s voltage law around each closed loop. This step yields simultaneous equations, one for each loop.
6. Apply Kirchhoff’s current law at a node that includes all of the branch currents of the network. This step gives one more simultaneous equation.
7. Solve the resulting simultaneous equations for the assumed branch currents.
8. If the solution of the equations yields positive current values, then the directions assumed in Step 3 are the actual directions. If any current value is negative, then the actual direction of the current is opposite to the assumed direction. It is not necessary to resolve the network using the true direction of current.
The Superposition Theorem
The superposition theorem simplifies the analysis of networks having more than one emf source. The theorem is stated as follows:
In any network containing more than one source of emf, the current through any branch is the algebraic sum of the currents produced by each source acting independently.
This theorem is applied in the following steps:
1. Select one source of emf. Replace all of the other sources with their internal resistances. If the internal resistance is 0, replace the source with a short circuit.
2. Calculate the magnitude and direction of the current in each branch due to the source of emf acting alone.
3. Repeat Steps 1 and 2 for each source of emf until the branch current components are calculated for all sources.
4. Find the algebraic sum of the component currents to obtain the true magnitude and direction of each branch current.
Thevenin’s Theorem
Thevenin’s theorem states that any two terminal networks containing resistances and sources of emf may be replaced by a single source of emf in series with a single resistance. The emf of the single source of emf, called ETH, is the open-circuit emf at the network terminal. The single series resistance, called RTH, is the resistance between the network terminals when all of the sources are replaced by their internal resistances.
When the Thevenin equivalent circuit is determined for a network, the process is known as thevenizing the circuit. Thevenin’s theorem is applied according to the following procedure:
1. Remove the load resistor and calculate the open-circuit terminal voltage of the network. This value is ETH.
2. Redraw the network with each source of emf replaced by a short circuit in series
with its internal resistance.
3. Calculate the resistance of the redrawn network as seen by looking back into the network from the output terminals. This value is RTH.
4. Draw the Thevenin equivalent circuit. This circuit consists of the series combination of ETH and RTH.
5. Connect the load resistor across the output terminals of the series circuit. This Thevenin circuit is equivalent to the original network. The advantage of thevenizing a circuit is that the load resistor can be varied without changing the Thevenin equivalent circuit. Changes in RL affect only the simple series Thevenin circuit. Therefore, the load current can be calculated easily for any number of values of RL.
Norton’s Theorem
Norton’s theorem reduces a circuit network into a simple current source and a single parallel resistance. Norton’s theorem can be applied as follows:
1. Place a short circuit across the load resistance and determine the Norton equivalent current, IN, based on the circuit voltage and series resistance.
2. Remove the short circuit from the load resistance and replace the power source with a short circuit.
3. Determine the Norton equivalent resistance, RN.
4. Connect the load resistance in parallel with the equivalent Norton current and
resistance.
5. Determine total resistance of the circuit.
6. Determine the voltage drop across the total resistance.
7. Use the determined voltage drop to compute the amount of current flow through the load resistance.
Achievement Review
For questions 1 through 4, calculate the magnitude and direction of the current through the resistor labeled RL. For added practice, try any of the methods described in this chapter.
.
5. Determine the total resistance of the circuit as seen by the voltage source.
Labels: Direct current fundamentals