LOAD ON A SYNCHRONOUS MOTOR
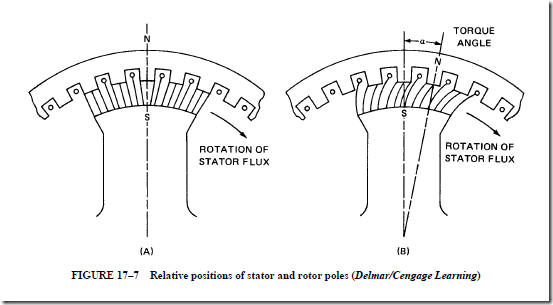
When the mechanical load is increased on a dc motor or an ac induction motor, there is a decrease in the speed. This decrease results in a reduction of the counterelectromotive force. Thus, the source can supply more current to meet the increased load demands. This method of compensating for an increased load cannot be used with a synchronous motor because the rotor must turn at synchronous speed at all loads. The relative positions of a stator pole and a rotor pole are shown at no load in Figure 17–7A for a synchronous motor. Note that the centers of both poles are in line with each other.
Once the rated load is applied, the relative positions of the stator pole and the rotor pole are as shown in Figure 17–7B. There is now an angular displacement of the rotor pole with respect to the stator pole. The speed is unchanged because the rotor will continue to rotate at synchronous speed. The angular displacement between the centers of the stator and rotor field poles is called the torque angle, a.
Operation with Different Loads
A synchronous motor operating at no load has a torque angle of nearly 0°. The counterelectromotive force in this case is almost equal to the impressed voltage (neglecting no– load motor losses). As the mechanical load increases, the torque angle increases. The phase angle between the impressed voltage and the counter-emf also increases. This increase allows the impressed voltage to cause more current in the stator windings to meet the additional load demands.
In Figure 17–8A, the counter emf is equal and opposite in direction to the impressed voltage at no load. The torque angle here is zero. The counter-emf shown in Fig- ure 17–8B is shifted by the angle a from its no-load position in Figure 17–8A. The shift is due to the addition of the load, which causes the rotor pole centers to shift behind the stator pole centers by the angle a. The line voltage and the counter-emf are not opposite each other at this point. The resultant voltage VR gives rise to the current IS in the stator windings. The stator windings have a high reactance, which causes current IS to lag the resultant voltage VR by nearly 90°. The power input for one phase of the three-phase motor is equal to
The synchronous motor can carry an increased mechanical load by shifting the relative positions of the stator and rotor poles. There is no decrease in the speed of the synchronous motor.
A serious overload will cause the angle between the centers of the stator and rotor poles to become too great. In this case, the rotor will pull out of synchronism. With the aid of the amortisseur winding, the motor will operate as an induction motor. The pull- out torque is the maximum torque value that can be developed by a synchronous motor
without dropping out of synchronism. For most synchronous motors, the pullout torque is 150% to 200% of the rated torque output.
POWER FACTOR
Changes in the dc field excitation do not affect the motor speed. However, such changes do alter the power factor of a synchronous motor. If all of the resistance of the rheostat is inserted in the field circuit, the field current drops below its normal value. A poor lagging power factor results. If the dc field is weak, the three-phase ac circuit to the stator supplies a magnetizing current to strengthen the field. This magnetizing component lags the voltage by 90 electrical degrees. The magnetizing current becomes a large part of the total current input. This gives rise to a low lagging power factor.
If a weak dc field is strengthened, the three-phase ac circuit to the stator supplies less magnetizing current. Because this current component becomes a smaller part of the total current input to the stator winding, the power factor increases. The field strength can be increased until the power factor is unity, or 100%. When the power factor reaches unity, the three-phase ac circuit supplies energy current only. The dc field circuit supplies all of the current required to magnetize the motor. The amount of dc field excitation required to obtain a unity power factor is called normal field excitation.
The magnetic field of the rotor can be strengthened still more by increasing the dc field current above the normal excitation value. The power factor in this case decreases. The circuit feeding the stator winding delivers a demagnetizing component of current. This current opposes the rotor field and weakens it until it returns to the normal magnetic strength.
Interaction between DC and AC Fields
Figure 17–9 shows how the magnetic field set up by the ac windings aids or opposes the dc field. The dc field is assumed to be stationary. The revolving armature is connected to the ac source. (In practice, most synchronous motors have stationary ac windings and a revolving dc field. However, the principle involved is the same.)
The dc excitation current is below its normal value in Figure 17–9A. The ac stator wind- ings supply a magnetizing component of current. This current lags the impressed voltage by 90°. This means that the current reaches its maximum value as shown. For this position, the flux created by the magnetizing component of current aids the weakened dc field. An in-phase component of current creates the torque required by the load. (This in-phase component is not shown in the figure.) The synchronous motor will have a lagging power factor because of the magnetizing component of current.
In Figure 17–9B, the dc excitation current is increased to its normal value. The ac input now supplies an in-phase current only. This current meets the torque requirements of the motor, but there is no magnetizing current component. Therefore, the power factor is unity.
The dc field is overexcited in Figure 17–9C. The ac input supplies a leading quadrature current that is really a demagnetizing component of current. This current sets up an mmf that opposes the mmf of the overexcited dc field. In this way, the dc field flux is limited to its normal full-strength value. Although not shown in Figure 17–8C, there is also an in-phase component of current. This in-phase component supplies the torque requirements
of the motor. When a synchronous motor with an overexcited dc field is supplied with a demagnetizing component of current (quadrature lead current), the motor has a leading power factor.
Typical Characteristic Curves
Typical characteristic curves for a synchronous motor with a constant mechanical load are shown in Figure 17–10. These curves show the changes that occur in the stator current and power factor as the dc field excitation current is varied.
At the normal dc field excitation current, the power factor has a peak value of unity. At the same point, the ac stator current is at its lowest value. As the field current is decreased, the power factor decreases in the lag quadrant. There is a resultant rise in the ac stator current. If the dc field current is increased above the normal field excitation value, the power factor decreases in the lead quadrant and the ac stator current increases.
Labels: Alternating current fundamentals