UNED CIRCUITS
LEARNING OBJECTIVES
Learning objectives are stated at the beginning of each chapter. These learning objectives serve as a preview of the information you are expected to learn in the chapter. The comprehensive check questions are based on the objectives. By successfully completing the OCC/ECC, you indicate that you have met the objectives and have learned the information. The learning objectives are listed below.
Upon completion of this chapter, you will be able to:
1. State the applications of a resonant circuit.
2. Identify the conditions that exist in a resonant circuit.
3. State and apply the formula for resonant frequency of an a.c. circuit.
4. State the effect of changes in inductance (L) and capacitance (C) on resonant frequency (fr).
5. Identify the characteristics peculiar to a series resonant circuit.
6. Identify the characteristics peculiar to a parallel resonant circuit.
7. State and apply the formula for Q.
8. State what is meant by the bandwidth of a resonant circuit and compute the bandwidth for a given circuit.
9. Identify the four general types of filters.
10. Identify how the series- and parallel-resonant circuit can be used as a band pass or a band-reject filter.
INTRODUCTION TO TUNED CIRCUITS
When your radio or television set is turned on, many events take place within the "receiver" before you hear the sound or see the picture being sent by the transmitting station.
Many different signals reach the antenna of a radio receiver at the same time. To select a station, the listener adjusts the tuning dial on the radio receiver until the desired station is heard. Within the radio or TV receiver, the actual "selecting" of the desired signal and the rejecting of the unwanted signals are accomplished by what is called a TUNED CIRCUIT. A tuned circuit consists of a coil and a capacitor connected in series or parallel. Later in this chapter you will see the application and advantages of both series- and parallel-tuned circuits. Whenever the characteristics of inductance and capacitance are found in a tuned circuit, the phenomenon as RESONANCE takes place.
You learned earlier in the Navy Electricity and Electronics Training Series, Module 2, chapter 4, that inductive reactance (XL) and capacitive reactance (XC) have opposite effects on circuit impedance (Z).
You also learned that if the frequency applied to an LCR circuit causes XL and XC to be equal, the circuit is RESONANT.
If you realize that XL and XC can be equal ONLY at ONE FREQUENCY (the resonant frequency), then you will have learned the most important single fact about resonant circuits. This fact is the principle that enables tuned circuits in the radio receiver to select one particular frequency and reject all others.
This is the reason why so much emphasis is placed on XL and X C in the discussions that follow.
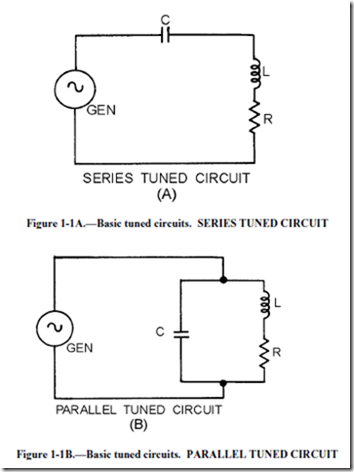
Examine figure 1-1. Notice that a basic tuned circuit consists of a coil and a capacitor, connected either in series, view (A), or in parallel, view (B). The resistance (R) in the circuit is usually limited to the inherent resistance of the components (particularly the resistance of the coil). For our purposes we are going to disregard this small resistance in future diagrams and explanations.
You have already learned how a coil and a capacitor in an a.c. circuit perform. This action will be the basis of the following discussion about tuned circuits.
Why should you study tuned circuits? Because the tuned circuit that has been described above is used in just about every electronic device, from remote-controlled model airplanes to the most sophisticated space satellite.
You can assume, if you are going to be involved in electricity or electronics, that you will need to have a good working knowledge of tuned circuits and how they are used in electronic and electrical circuits.
REVIEW OF SERIES/PARALLEL A.C. CIRCUITS
First we will review the effects of frequency on a circuit which contains resistance, inductance, and capacitance. This review recaps what you previously learned in the Inductive and Capacitive Reactance chapter in module 2 of the NEETS.
FREQUENCY EFFECTS ON RLC CIRCUITS
Perhaps the most often used control of a radio or television set is the station or channel selector. Of course, the volume, tone, and picture quality controls are adjusted to suit the individual's taste, but very often they are not adjusted when the station is changed. What goes on behind this station selecting? In this chapter, you will learn the basic principles that account for the ability of circuits to "tune" to the desired station.
Effect of Frequency on Inductive Reactance
In an a.c. circuit, an inductor produces inductive reactance which causes the current to lag the voltage by 90 degrees. Because the inductor "reacts" to a changing current, it is known as a reactive component. The opposition that an inductor presents to a.c. is called inductive reactance (X L). This opposition is caused by the inductor "reacting" to the changing current of the a.c. source. Both the inductance and the frequency determine the magnitude of this reactance. This relationship is stated by the formula:

As shown in the equation, any increase in frequency, or "f," will cause a corresponding increase of inductive reactance, or "XL." Therefore, the INDUCTIVE REACTANCE VARIES DIRECTLY WITH THE FREQUENCY. As you can see, the higher the frequency, the greater the inductive reactance; the lower the frequency, the less the inductive reactance for a given inductor. This relationship is illustrated in figure 1-2. Increasing values of XL are plotted in terms of increasing frequency. Starting at the lower left corner with zero frequency, the inductive reactance is zero. As the frequency is increased (reading to the
right), the inductive reactance is shown to increase in direct proportion.
Effect of Frequency on Capacitive Reactance
In an a.c. circuit, a capacitor produces a reactance which causes the current to lead the voltage by 90 degrees. Because the capacitor "reacts" to a changing voltage, it is known as a reactive component. The opposition a capacitor presents to a.c. is called capacitive reactance (XC). The opposition is caused by the capacitor "reacting" to the changing voltage of the a.c. source. The formula for capacitive reactance is:

In contrast to the inductive reactance, this equation indicates that the CAPACITIVE REACTANCE VARIES INVERSELY WITH THE FREQUENCY. When f = 0, XC is infinite () and decreases as frequency increases. That is, the lower the frequency, the greater the capacitive reactance; the higher the frequency, the less the reactance for a given capacitor.
As shown in figure 1-3, the effect of capacitance is opposite to that of inductance. Remember, capacitance causes the current to lead the voltage by 90 degrees, while inductance causes the current to lag the voltage by 90 degrees.

In the expression for inductive reactance, XL = 2fL, and in the expression for capacitive reactance,
both contain "f" (frequency). Any change of frequency changes the reactance of the circuit components as already explained. So far, nothing has been said about the effect of frequency on resistance. In an Ohm's law relationship, such as R = E/I no "f" is involved. Thus, for all practical purposes, a change of frequency does not affect the resistance of the circuit. If a 60-hertz a.c. voltage causes 20 milliamperes of current in a resistive circuit, then the same voltage at 2000 hertz, for example, would still cause 20 milliamperes to flow.
NOTE: Remember that the total opposition to a.c. is called impedance (Z). Impedance is the combination of inductive reactance (XL), capacitive reactance (XC), and resistance (R). When dealing with a.c. circuits, the impedance is the factor with which you will ultimately be concerned. But, as you have just been shown, the resistance (R) is not affected by frequency. Therefore, the remainder of the discussion of a.c. circuits will only be concerned with the reactance of inductors and capacitors and will ignore resistance.
Labels: Wave-Generation and Wave-Shaping