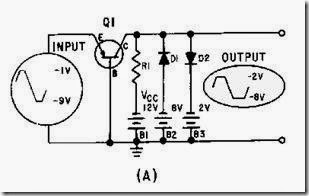
The common-base transistor clamper is similar to the dual diode limiter in figure 4-15, except for the addition of a transistor. In the previous clampers, we have clamped the output signal to a reference. In the transistor common-base clamper, we want to clamp the amplitude of the input to no more than nor less than certain values in the output. Also, we do not want phase inversion in the output. View (A) of figure 4-24 shows such a circuit. The transistor does not amplify the input and the output is not inverted. However, the two diode circuits serve to clamp the output between -2 volts and -8 volts, no matter what the varying input positive and negative extremes.
Figure 4-24A.—Common-base configuration clamper.
Figure 4-24B.—Common-base configuration clamper.
Look at view (B) as we continue. The input signal is a square-wave pulse type signal that varies in amplitude. Without an input signal, Q1 conducts and provides current through R1. This develops the output (collector to ground) potential which is assumed to be approximately -5 volts (VCC - ER1) for this discussion.
From T0 to T1 the output follows the input because of the increasing emitter-base forward bias. However, at T1 the collector voltage reaches -2 volts and D2 is forward biased. D2 conducts and limits the output to -2 volts (the value of B3). D2 conducts until T2 when the input decreases below -2 volts. At this time, D2 cuts off and the output again follows the input because of the decreasing forward bias on Q1. At T3 the input reaches -8 volts and forward biases D1. D1 conducts and any further increase (beyond -8 volts) of the input has no effect on the output. When the input returns to a value more positive than -8 volts, D1 cuts off and the output again follows the input. This circuit action is the same for all inputs. The output remains the same as the input except that both positive and negative extremes are clamped at -2 and -8 volts, respectively.
Timing circuits and circuits which require a particular shape or "spike" of voltage, may use SHAPING circuits. Shaping circuits can be used to cause wave shapes, such as square waves, sawtooth waves, and trapezoidal waves, to change their shape. Shaping circuits may be either series RC or series RL circuits. The time constant is controlled in respect to the duration of the applied waveform. Notice that the wave shapes mentioned did not include the sine wave. These RC or RL shaping circuits do not change the shape of a pure sine wave.
The series RC and RL circuits electrically perform the mathematical operations of INTEGRATION and DIFFERENTIATION. Therefore, the circuits used to perform these operations are called INTEGRATORS and DIFFERENTIATORS. These names are applied to these circuits even though they do not always completely perform the operations of mathematical integration and differentiation.
Pure sine waves are basic wave shapes from which other wave shapes can be constructed. Any waveform that is not a pure sine wave consists of two or more sine waves. Adding the correct frequencies at the proper phase and amplitude will form square waves, sawtooth waves, and other nonsinusoidal waveforms.
A waveform other than a sine wave is called a COMPLEX WAVE. You will see that a complex wave consists of a fundamental frequency plus one or more HARMONIC frequencies. The shape of a nonsinusoidal waveform is dependent upon the type of harmonics present as part of the waveform, their relative amplitudes, and their relative phase relationships. In general, the steeper the sides of a waveform, that is, the more rapid its rise and fall, the more harmonics it contains.
The sine wave which has the lowest frequency in the complex periodic wave is referred to as the FUNDAMENTAL FREQUENCY. The type and number of harmonics included in the waveform are dependent upon the shape of the waveform. Harmonics have two classifications — EVEN numbered and ODD numbered. Harmonics are always a whole number of times higher than the fundamental frequency and are designated by an integer (whole number). For example, the frequency twice as high as the fundamental frequency is the SECOND HARMONIC (or the first even harmonic).
View (A) of figure 4-25 compares a square wave with sine waves. Sine wave K is the same frequency as the square wave (its fundamental frequency). If another sine wave (L) of smaller amplitude but three times the frequency (referred to as the third harmonic) is added to sine wave K, curve M is produced. The addition of these two waveforms is accomplished by adding the instantaneous values of both sine waves algebraically. Curve M is called the resultant. Notice that curve M begins to assume the shape of a square wave. Curve M is shown again in view (B).
As shown in view (B), when the fifth harmonic (curve N with its decreased amplitude) is added, the sides of the new resultant (curve P) are steeper than before. In view (C), the addition of the seventh harmonic (curve Q), which is of even smaller amplitude, makes the sides of the composite waveform (R) still steeper. The addition of more odd harmonics will bring the composite waveform nearer the shape of the perfect square wave. A perfect square wave is, therefore, composed of an infinite number of odd harmonics. In the composition of square waves, all the odd harmonics cross the reference line in phase with the fundamental.
A sawtooth wave, shown in figure 4-26, is made up of both even and odd harmonics. Notice that each higher harmonic is added in phase as it crosses the 0 reference in view (A), view (B), view (C), and view (D). The resultant, shown in view (D), closely resembles a sawtooth waveform.
Figure 4-26A.—Composition of a sawtooth wave.
Figure 4-26B.—Composition of a sawtooth wave.
Figure 4-26C.—Composition of a sawtooth wave.
Figure 4-26D.—Composition of a sawtooth wave.
Figure 4-27 shows the composition of a peaked wave. Notice how the addition of each odd harmonic makes the peak of the resultant higher and the sides steeper. The phase relationship between the harmonics of the peaked wave is different from the phase relationship of the harmonics in the composition of the square wave. In the composition of the square wave, all the odd harmonics cross the
reference line in phase with the fundamental. In the peaked wave, harmonics such as the third, seventh, and so forth, cross the reference line 180 degrees out of phase with the fundamental; the fifth, ninth, and so forth, cross the reference line in phase with the fundamental.
Q15. What is the harmonic composition of a square wave? Q16. What is the peaked wave composed of?
Q17. What is the fundamental difference between the phase relationship of the harmonics of the square wave as compared to the harmonics of a peaked wave?
Labels: Wave-Generation and Wave-Shaping