
Algorithm:
ALGORITHM Kruskal (G)
//Kruskal’s algorithm for constructing a MST
//Input: A weighted connected graph G = { V, E }
//Output: ET the set of edges composing a MST of G
Sort E in ascending order of the edge weights
// initialize the set of tree edges and its size
STEP 1: Sort the edges by increasing weight
STEP 2: Start with a forest having |V| number of trees.
STEP 3: Number of trees are reduced by ONE at every inclusion of an edge At each stage:
• Among the edges which are not yet included, select the one with minimum weight AND which does not form a cycle.
• the edge will reduce the number of trees by one by combining two trees of the forest
Apply Kruskal’s algorithm for the following graph to find MST.
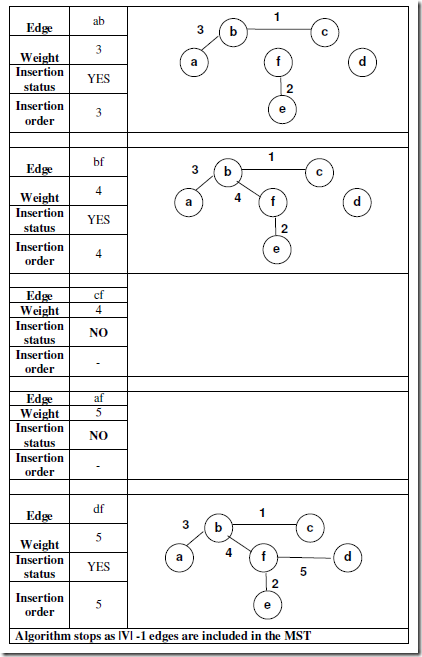
Efficiency:
Efficiency of Kruskal’s algorithm is based on the time needed for sorting the edge weights of a given graph.
• With an efficient sorting algorithm: Efficiency: Θ(|E| log |E| )