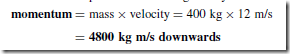
The momentum of a body is defined as the product of its mass and its velocity, i.e. momentum = mu, where m D mass (in kg) and u D velocity (in m/s). The unit of momentum is kg m/s.
Since velocity is a vector quantity, momentum is a vector quantity, i.e.
it has both magnitude and direction.
For example, the momentum of a pile driver of mass 400 kg when it is moving downwards with a speed of 12 m/s is given by:
Newton’s first law of motion states:
a body continues in a state of rest or in a state of uniform motion in a straight line unless acted on by some external force
Hence the momentum of a body remains the same provided no external forces act on it.
The principle of conservation of momentum for a closed system (i.e. one on which no external forces act) may be stated as:
the total linear momentum of a system is a constant
The total momentum of a system before collision in a given direction is equal to the total momentum of the system after collision in the same direction. In Figure 27.1, masses m1 and m2 are travelling in the same direction with velocity u1 > u2 . A collision will occur, and applying the principle of conservation of momentum:
total momentum before impact D total momentum after impact
For example, a wagon of mass 10 t is moving at a speed of 6 m/s and collides with another wagon of mass 15 t, which is stationary. After impact, the wagons are coupled together. To determine the common velocity of the wagons after impact:
i.e. the common velocity after impact is 2.4 m/s in the direction in which the 10 t wagon is initially travelling.
Impulse and Impulsive Forces
Newton’s second law of motion states:
the rate of change of momentum is directly proportional to the applied force producing the change, and takes place in the direction of this force
In the SI system, the units are such that:
the applied force D rate of change of momentum
When a force is suddenly applied to a body due to either a collision with another body or being hit by an object such as a hammer, the time taken in equation (1) is very small and difficult to measure. In such cases, the total effect of the force is measured by the change of momentum it produces.
Forces that act for very short periods of time are called impulsive forces. The product of the impulsive force and the time during which it acts is called
the impulse of the force and is equal to the change of momentum produced by the impulsive force, i.e.
impulse = applied force × time = change in linear momentum
For example, the average force exerted on the work-piece of a press-tool operation is 150 kN, and the tool is in contact with the work-piece for 50 ms.
From above,
Examples where impulsive forces occur include when a gun recoils and when a free-falling mass hits the ground. Solving problems associated with such occurrences often requires the use of the equation of motion: v2 D u2 C 2as, from Chapter 15.
For example, the hammer of a pile-driver of mass 1 t falls a distance of 1.5 m on to a pile. The blow takes place in 25 ms and the hammer does not rebound.
Since the impulsive force is the rate of change of momentum, the average force exerted on the pile is 217 kN
When a pile is being hammered into the ground, the ground resists the movement of the pile and this resistance is called a resistive force.
Newton’s third law of motion may be stated as:
for every force there is an equal and opposite force
The force applied to the pile is the resistive force; the pile exerts an equal and opposite force on the ground.
In practice, when impulsive forces occur, energy is not entirely conserved and some energy is changed into heat, noise, and so on.
When two equal forces act on a body as shown in Figure 28.1, they cause the body to rotate, and the system of forces is called a couple.
The turning moment of a couple is called a torque, T. In Figure 28.1,
The unit of torque is the newton metre, Nm
When a force F newtons is applied at a radius r metres from the axis of, say, a nut to be turned by a spanner, as shown in Figure 28.2, the torque T applied to the nut is given by: T = Fr Nm
For example, the torque when a pulley wheel of diameter 300 mm has a force of 80 N applied at the rim, is given by:
Work Done and Power Transmitted by a Constant Torque
Figure 28.3(a) shows a pulley wheel of radius r metres attached to a shaft and a force F newtons applied to the rim at point P
Figure 28.3(b) shows the pulley wheel having turned through an angle (} radians as a result of the force F being applied. The force moves through a distance s, where arc length
From above, work done D T(}, and if this work is available to increase the kinetic energy of a rotating body of moment of inertia I, then:
where I is the moment of inertia in kg m2, ˛ is the angular acceleration in rad/s2 and T is the torque in Nm.
For example, if a shaft system has a moment of inertia of 37.5 kg m2, the torque required to give it an angular acceleration of 5.0 rad/s2 is given by:
Power Transmission by Belt Drives
A common and simple method of transmitting power from one shaft to another is by means of a belt passing over pulley wheels which are keyed to the shafts, as shown in Figure 28.4. Typical applications include an electric motor driving a lathe or a drill, and an engine driving a pump or generator.
For a belt to transmit power between two pulleys there must be a difference in tensions in the belt on either side of the driving and driven pulleys. For the direction of rotation shown in Figure 28.4, F2 > F1
The torque T available at the driving wheel to do work is given by:
and the available power P is given by:
For example, a 15 kW motor is driving a shaft at 1150 rev/min by means of pulley wheels and a belt. The tensions in the belt on each side of the driver pulley wheel are 400 N and 50 N. The diameters of the driver and driven pulley wheels are 500 mm and 750 mm respectively. The power output from the motor is given by:
Flat and V-belts
The ratio of the tensions for a flat belt when the belt is on the point of slipping is:
where 11 is the coefficient of friction between belt and pulley, (} is the angle of lap, in radians (see Figure 28.5), and e is the exponent ³ 2.718
For a vee belt as in Figure 28.6, the ratio is:
where ˛ is the half angle of the groove and of the belt.
This gives a much larger ratio than for the flat belt. The V-belt is jammed into its groove and is less likely to slip. Referring to Figure 28.6, the force of friction on each side is 11RN where RN is the normal (perpendicular) reaction
on each side. The triangle of forces shows that 
The corresponding force of friction for a flat belt is 11R. Comparing the forces of friction for flat and V-belts it can be said that the V-belt is equivalent to a flat belt with a coefficient of friction given by
The net force exerted on the belt by a driving pulley, or the belt on a driven pulley is T1 Ł T2. The power transmitted by a belt is therefore (T1 Ł T2)v, where v is the speed of the belt. If (T1 Ł T2) is measured in newtons and v in metres per second, the power will be Nm/s, i.e. watts (W).
The belt speed is given in m/s by ωr, where ω is the angular speed of the pulley (rad/s) and r is its radius (m).
It should be noted that:
(a) slipping would be expected to occur first on the pulley having the smaller angle of lap
(b) in practice, care would be taken to ensure that slipping is not likely to
occur.
For example, a pulley has vee grooves to take six belts which are required to transmit 125 kW from the pulley when its speed is 1920 rev/min. The angle of the grooves is 45° , the angle of lap is 175° and the effective diameter of the pulley is 265 mm. If the coefficient of friction is 0.32, the lowest possible value for the tension on the tight side of each belt is calculated as follows:
The power transmitted by the six belts is given by: 6(T1 Ł T2)v where T1 and T2 are the tensions on the tight and slack sides respectively of one belt, and v (D ωr) is the belt speed,
