A permanent magnet is a piece of ferromagnetic material (such as iron, nickel or cobalt) that has properties of attracting other pieces of these materials. A permanent magnet will position itself in a north and south direction when freely suspended. The north-seeking end of the magnet is called the north pole, N, and the south-seeking end the south pole, S.
The area around a magnet is called the magnetic field and it is in this area that the effects of the magnetic force produced by the magnet can be detected. A magnetic field cannot be seen, felt, smelt or heard and therefore is difficult to represent. Michael Faraday suggested that the magnetic field could be represented pictorially, by imagining the field to consist of lines of magnetic flux, which enables investigation of the distribution and density of the field to be carried out.
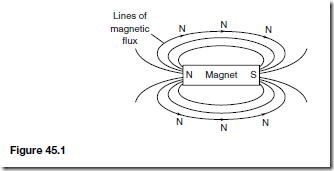
The distribution of a magnetic field can be investigated by using some iron filings. A bar magnet is placed on a flat surface covered by, say, cardboard, upon which is sprinkled some iron filings. If the cardboard is gently tapped the filings will assume a pattern similar to that shown in Figure 45.1. If a number of magnets of different strength are used, it is found that the stronger the field the closer are the lines of magnetic flux and vice versa. Thus a magnetic field has the property of exerting a force, demonstrated in this case by causing the iron filings to move into the pattern shown. The strength of the magnetic field decreases as we move away from the magnet. It should be realised, of course, that the magnetic field is three dimensional in its effect, and not acting in one plane as appears to be the case in this experiment.
If a compass is placed in the magnetic field in various positions, the direction of the lines of flux may be determined by noting the direction of the compass pointer. The direction of a magnetic field at any point is taken as that in which the north-seeking pole of a compass needle points when suspended in the field. The direction of a line of flux is from the north pole to the south pole on the outside of the magnet and is then assumed to continue through the magnet back to the point at which it emerged at the north pole. Thus such lines of flux always form complete closed loops or paths, they never intersect and always have a definite direction.
The laws of magnetic attraction and repulsion can be demonstrated by using two bar magnets. In Figure 45.2(a), with unlike poles adjacent, attraction takes place. Lines of flux are imagined to contract and the magnets try to pull together. The magnetic field is strongest in between the two magnets, shown by the lines of flux being close together. In Figure 45.2(b), with similar poles adjacent (i.e. two north poles), repulsion occurs, i.e. the two north poles try to push each other apart, since magnetic flux lines running side by side in the same direction repel.
Magnetic flux is the amount of magnetic field (or the number of lines of force) produced by a magnetic source. The symbol for magnetic flux is (Greek letter ‘phi’). The unit of magnetic flux is the weber, Wb.
Magnetic flux density is the amount of flux passing through a defined area that is perpendicular to the direction of the flux:
Magnetomotive force (m.m.f.) is the cause of the existence of a magnetic flux in a magnetic circuit,
where N is the number of conductors (or turns) and I is the current in amperes. The unit of m.m.f. is sometimes expressed as ‘ampere-turns’. However since ‘turns’ have no dimensions, the S.I. unit of m.m.f. is the ampere.
For example, a magnetising force of 8000 A/m is applied to a circular magnetic circuit of mean diameter 30 cm by passing a current through a coil wound on the circuit. The coil is uniformly wound around the circuit and has 750 turns. To determine the current in the coil:
For air, or any non-magnetic medium, the ratio of magnetic flux density to magnetising force is a constant, i.e. B/H D a constant. This constant is f.L0 , the permeability of free space (or the magnetic space constant) and is equal 10Ł7 H/m, i.e. for air, or any non-magnetic medium,
(Although all non-magnetic materials, including air, exhibit slight magnetic properties, these can effectively be neglected.)
For all media other than free space,
where ur is the relative permeability, and is defined as
varies with the type of magnetic material and, since it is a ratio of flux densities, it has no unit. From its definition, f.Lr for a vacuum is 1.
By plotting measured values of flux density B against magnetic field strength H, a magnetisation curve (or B-H curve) is produced. For non-magnetic materials this is a straight line. Typical curves for four magnetic materials are shown in Figure 45.3
For example, a uniform ring of cast iron has a cross-sectional area of 10 cm2 and a mean circumference of 20 cm. The m.m.f. necessary to produce a flux of 0.3 mWb in the ring is determined as follows:
The relative permeability of a ferromagnetic material is proportional to the slope of the B-H curve and thus varies with the magnetic field strength. The approximate range of values of relative permeability f.Lr for some common magnetic materials are:
For example, a flux density of 1.2 T is produced in a piece of cast steel by a magnetising force of 1250 A/m. The relative permeability of the steel under these conditions is determined using
Reluctance S (or RM ) is the ‘magnetic resistance’ of a magnetic circuit to the presence of magnetic flux.
The unit of reluctance is 1/H (or H-1) or A/Wb.
For example, the reluctance of a piece of mumetal of length 150 mm and cross-sectional area 1800 mm2 when the relative permeability is 4000 is given by:
Ferromagnetic materials have a low reluctance and can be used as magnetic screens to prevent magnetic fields affecting materials within the screen.
For a series magnetic circuit having n parts, the total reluctance S is given by:
S = S1 + S2 + ··· + Sn
(This is similar to resistors connected in series in an electrical circuit) For example, a closed magnetic circuit of cast steel contains a 6 cm long path of cross-sectional area 1 cm2 and a 2 cm path of cross-sectional area 0.5 cm2. A coil of 200 turns is wound around the 6 cm length of the circuit and a current of 0.4 A flows. If the relative permeability of the cast steel is 750 the flux density in the 2 cm path is determined as follows:
For the 6 cm long path:
Comparison between Electrical and Magnetic Quantities
Let a ferromagnetic material which is completely demagnetised, i.e. one in which B D H D 0, be subjected to increasing values of magnetic field strength H and the corresponding flux density B measured. The resulting relationship between B and H is shown by the curve Oab in Figure 45.4. At a particular value of H, shown as Oy, it becomes difficult to increase the flux density any further. The material is said to be saturated. Thus by is the saturation flux density.
If the value of H is now reduced it is found that the flux density follows curve bc. When H is reduced to zero, flux remains in the iron. This
remanent flux density or remanence is shown as Oc in Figure 45.4. When H is increased in the opposite direction, the flux density decreases until, at a value shown as Od, the flux density has been reduced to zero. The magnetic field strength Od required to remove the residual magnetism, i.e. reduce B to zero, is called the coercive force.
Further increase of H in the reverse direction causes the flux density to increase in the reverse direction until saturation is reached, as shown by curve de. If H is varied backwards from Ox to Oy, the flux density follows the curve efgb, similar to curve bcde.
It is seen from Figure 45.4 that the flux density changes lag behind the changes in the magnetic field strength. This effect is called hysteresis. The closed figure bcdefgb is called the hysteresis loop (or the B/H loop).
A disturbance in the alignment of the domains (i.e. groups of atoms) of a ferromagnetic material causes energy to be expended in taking it through a cycle of magnetisation. This energy appears as heat in the specimen and is called the hysteresis loss The energy loss associated with hysteresis is proportional to the area of the hysteresis loop.
If the hysteresis loop is plotted to a scale of 1 cm D ˛ ampere/metre along the horizontal axis and 1 cm D ˇ tesla along the vertical axis, and if A repre- sents the area of the loop in square centimetres, then
The maximum sized hysteresis loop for a particular material is obtained at saturation. If, for example, the maximum flux density is reduced to half its value at saturation, the area of the resulting loop is considerably less than the area of the loop at saturation. From the areas of a number of such hysteresis loops, as shown in Figure 45.5, the hysteresis loss per cycle was found by Steinmetz (an American electrical engineer) to be proportional to (Bm )n, where n is called the Steinmetz index and can have a value between about 1.6 and 3.0, depending on the quality of the ferromagnetic material and the range of flux density over which the measurements are made.
It is found that the hysteresis loss is given by:
where v D volume in cubic metres, f D frequency in hertz, and kh is a constant for a given specimen and given range of B.
For example, if a ferromagnetic specimen has a hysteresis loss of 62500 Wb/m3 when the maximum flux density is 1.5 T at a frequency of 50 Hz, then the hysteresis loss per m3 for a maximum flux density of 1.1 T and frequency of 25 Hz, assuming the Steinmetz index to be 1.6, is determined as follows:
The magnitude of the hysteresis loss depends on the composition of the specimen and on the heat treatment and mechanical handling to which the specimen has been subjected.
Figure 45.6 shows typical hysteresis loops for (a) hard steel, which has a high remanence Oc and a large coercivity Od, (b) soft steel, which has a large remanence and small coercivity and (c) ferrite, this being a ceramic- like magnetic substance made from oxides of iron, nickel, cobalt, magnesium, aluminium and manganese. The hysteresis of ferrite is very small.
For a.c.-excited devices the hysteresis loop is repeated every cycle of alternating current. Thus a hysteresis loop with a large area (as with hard steel) is often unsuitable since the energy loss would be considerable.
Silicon steel has a narrow hysteresis loop, and thus small hysteresis loss, and is suitable for transformer cores and rotating machine armatures.
If a coil is wound on a ferromagnetic core (such as in a transformer) and alternating current is passed through the coil, an alternating flux is set up in the core. The alternating flux induces an e.m.f. e in the coil given by:
However, in addition to the desirable effect of inducing an e.m.f.
in the coil, the alternating flux induces undesirable voltages in the iron core.
These induced e.m.f.’s set up circulating currents in the core, known as eddy currents. Since the core possesses resistance, the eddy currents heat the core, and this represents wasted energy.
Eddy currents can be reduced by laminating the core, i.e. splitting it into thin sheets with very thin layers of insulating material inserted between each pair of the laminations (this may be achieved by simply varnishing one side of the lamination or by placing paper between each lamination). The insulation presents a high resistance and this reduces any induced circulating currents.
From equation (4) it is seen that eddy current loss is proportional to the square of the thickness of the core strip. It is therefore desirable to make lamination strips as thin as possible. However, at high frequencies where it is not practicable to make very thin laminations, using ferrite or dust cores may reduce core losses. Dust cores consist of fine particles of carbonyl iron or permalloy (i.e. nickel and iron), each particle of which is insulated from its neighbour by a binding material. Such materials have a very high value of resistivity.
For example, the core of a transformer operating at 50 Hz has an eddy current loss of 100 W/m3and the core laminations have a thickness of 0.50 mm. The core is redesigned so as to operate with the same eddy current loss but at a different voltage and at a frequency of 250 Hz. Assuming that at the new voltage the maximum flux density is one-third of its original value and the resistivity of the core remains unaltered, the necessary new thickness of the laminations is determined as follows:
From equation (4), Pe D ke(Bm )2 f2t2 watts per m3.
Hence, at 50 Hz frequency, 100 D ke(Bm )2 (50)2 (0.50 ð 10Ł3 )2 from 100
Separation of Hysteresis and Eddy Current Losses
which is of the straight line form y D mx C c. Thus if Pc /f is plotted vertically against f horizontally, a straight line graph results having a gradient k2 and a vertical-axis intercept k1
If the total core loss Pc is measured over a range of frequencies, then k1 and k2 may be determined from the graph of Pc /f against f. Hence the hysteresis loss Ph (D k1f) and the eddy current loss Pe(D k2f2) at a given frequency may be determined.
The above method of separation of losses is an approximate one since the Steinmetz index n is not a constant value but tends to increase with increase of frequency. However, a reasonable indication of the relative magnitudes of the hysteresis and eddy current losses in an iron core may be determined.
For example, the total core loss of a ferromagnetic cored transformer winding is measured at different frequencies and the results obtained are: