Scalars and Vectors
Quantities used in engineering and science can be divided into two groups:
(a) Scalar quantities have a size (or magnitude) only and need no other information to specify them. Thus, 10 centimetres, 50 seconds, 7 litres, 3 kilograms, 25°C, £250, 10 cm3 volume and 10 joules of energy, are all examples of scalar quantities.
(b) Vector quantities have both a size or magnitude and a direction, called the line of action of the quantity. Thus, a velocity of 50 kilometers per hour due east, an acceleration of 9.81 meters per second squared vertically downwards, a force of 15 newtons at an angle of 30 degrees, and a north- westerly wind of 15 knots are all examples of vector quantities.
The speed of a body can be stated without reference to the direction of movement of that body. Thus, speed is a scalar quantity. If, however, we specify the direction of motion as well as the speed of the body, the quantity is then termed the velocity of the body. Velocity is thus a vector quantity.
A weight of, say, 20 newtons, might initially appear to be a scalar quantity; however, weight also has a direction, i.e. downwards (towards the center of the earth). Thus, weight is a vector quantity.
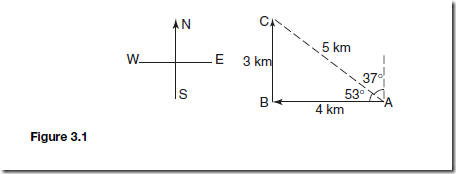
When we say a man has walked 7 km we give no indication of direction. Thus, distance is a scalar quantity. If, however, the man walks 4 km westwards, then 3 km northwards as shown in Figure 3.1, his final position at C is 5 km away from his initial position at A (by Pythagoras’ theorem). This change in position is called displacement. Thus 7 km is the distance walked, and 5 km in a direction N37°W is a vector quantity.
Summarising, a quantity that has magnitude and direction is a vector quantity, whereas a quantity that has magnitude only is a scalar quantity.
Vector Representation
A vector may be represented by a straight line, the length of line being directly proportional to the magnitude of the quantity and the direction of the line being
in the same direction as the line of action of the quantity. An arrow is used to denote the sense of the vector, that is, for a horizontal vector, say, whether it acts from left to right or vice-versa. The arrow is positioned at the end of the vector and this position is called the ‘nose’ of the vector. Figure 3.2 shows a velocity of 20 m/s at an angle of 45° to the horizontal and may be depicted by oa D 20 m/s at 45° to the horizontal.
To distinguish between vector and scalar quantities, various ways are used. These include:
(i) bold print,
(ii) two capital letters with an arrow above them to denote the sense of direc- tion, e.g. ðA!B, where A is the starting point and B the end point of the vector,
(iii) a line over the top of letters, e.g. AB or a
(iv) letters with an arrow above, e.g. aE, AE
(v) underlined letters, e.g. a
(vi) xi C jy, where i and j are axes at right-angles to each other; for example, 3i C 4j means 3 units in the i direction and 4 units in the j direction, as shown in Figure 3.3
(vii) a column matrix ( a \b); for example, the vector OA shown in Figure 3.3could be represented by ( 3 \4)
Thus, OA represents a vector quantity, but OA is the magnitude of the vector OA. Also, positive angles are measured in an anticlockwise direction from a horizontal, right facing line, and negative angles in a clockwise direction from this line — as with graphical work. Thus 90° is a line vertically upwards and ð90° is a line vertically downwards.