The parallelogram and triangle of forces

Resultant force

When two or more forces are acting together at a point it is always possible to find a single force which will have exactly the same effect as these forces.
This single force is called the resultant force.

Where a number of forces are all acting in the same straight line, the task of finding their resultant becomes simply a matter of addition or subtraction. Thus, if forces of 7, 5, 3 and 1 N act at a point P as shown in the image, we have,

Resultant force

Forces acting in the same straight line:

Total forces acting towards the left = 7 + 5 = 12 N

Total forces acting towards the right = 3 +1 = 4 N
resultant force = 12 – 4 = 8 N acting towards the left.

Graphical representation of force

Vectors can always be represented by straight lines drawn to scale. Thus if two forces of 5 and 7 N act at right angles to one another we can represent them on a scale of 1 cm to 1 N by drawing two lines at right angles which are respectively 5 and 7 cm long – You can revise this article for more information about scalars and vectors: Speed,velocity and acceleration from scratch -.

We’ll show now how to find the resultant of two forces which act at a point, but are not in the same direction.
Side note: In order to save your time, you can save this article as a pdf book (small book ).

To verify the parallelogram of forces

· A drawing-board with a sheet of paper pinned to it is set up vertically with two freely running pulleys clamped to the top.

Parallelogram of forces

Parallelogram of forces diagram:

A length of thread having a 50 N weight at one end and a 70 N weight at the other is passed over the two pulleys and a second length of thread carrying a 100 N weight is tied to the first at O.
The thread will take up a position for which the three forces acting at O are in equilibrium.

Small pencil crosses are now made on the paper, as far apart as possible, to make the positions of the threads.
A fairly accurate method of doing this is to make the positions of the shadows of the threads formed either by the sun or a distant lamp.

· The paper is now removed from the board and the crosses joined by pencil lines to represent the force directions.
Next, using a scale of 1 cm to represent 10 N, distances OP = 5 cm, OQ = 7 cm and OE = 10 cm are marked off to represent the three forces of 50, 70, and 100 N acting at O.

          Also, OE is produced and OR = 10 cm is marked off along it.
          Clearly, the forces OP and OQ together are balanced by force OE.
          Hence, the resultant of OP and OQ must be a force equal and opposite to OE.

But we have made OR equal and opposite to OE and hence OR must be the resultant of OP and OQ.

If now, PR and QR are joined, the opposite sides of figure PRQO may be tested with a set-square and ruler and shown to be parallel. It follows that PRQO is a parallelogram, and this is found to be the case for all values of the forces used in this experiment, provided that any one of them is not greater than the sum of the other two. The experiment illustrates an important principle called,

The parallelogram of forces principle

If two forces acting at a point are represented both in magnitude and direction by the adjacent sides of a parallelogram, their resultant will be represented both in magnitude and direction by the diagonal of the parallelogram drawn from the point.

Resultant of two forces: Worked examples

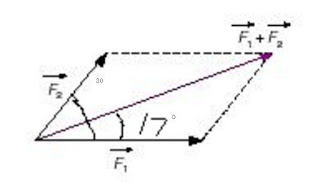
1- A linear is towed into harbor by two tugs A and B whose cables make an angle of 30°. If A exerts a pull of 2.5 N, and B a pull of 3.2 N, find, graphically, the resultant pull on the linear and the angle it makes with the cable of the weaker tug.

Solution method:

Any convenient length may be used to represent 1 N, but it should be chosen so as to give us large a diagram as possible – See image below- .

Now, two lines represent the two forces acting on the linear: 2.50 N and 3.20 N are drawn at an angle of 30°.
On completing the parallelogram by the usual geometrical construction, the diagonal is found by measurement to be 5.5 units long and makes an angle of 17° with LA.
Therefore, resultant pull on liner = 5.5 N
and angle made with cable of weaker tug = 17°.

2. Find graphically or otherwise the resultant of two forces of 7 N and 3 N, acting at a point and at right angles to one another.

Solution method diagram:

Resultant of two forces at right angles

The problem may be solved graphically by drawing a scale diagram as in the previous example or, alternatively, the resultant may be calculated using Pythagoras’ theorem: “The sum of the areas of the two squares on the legs equals the area of the square on the hypotenuse
a² + b² = c²”.

Thus, if OP and OQ represent the two forces of 3 and 7 N respectively, the resultant force will be represented by the diagonal OR of the rectangle OPRQ.

By Pythagoras’ theorem,

OR² = OP² + OQ²
= 3² + 7² = 9 + 49 = 58

hence, OR = √58 = 4.6 Newton.
also, if Θ is the angle ROQ, tan Θ = 3/7 = 0.4286
Therefore, Θ = 23° 12’ .

**It follows that the resultant is a force of 7.6 N in direction making an angle of 23° 12’ with the 7 N force.**

Resolution of forces

We have just seen how the principle of the parallelogram of forces enables us to find the resultant of two forces acting at a point at an angle to one another. However, it is very often necessary to be able to carry out the reverse process and convert a single force into two component forces. When this is done, the force is said to have been resolved into two components.
For most practical purposes a force is resolved along two directions at right angles.

towed-barge

Force on sailing

The image shows the forces involved when a barge is being towed along a canal by a horse. Before the advent of railways, this was an important mode of transport in England during the eighteenth and nineteenth centuries.

Worked example:
A garden roller is pulled with a force of 20 N acting at right angle of 50° with the ground level. Find the effective force pulling the roller along the ground.
Solution
As a rule, problems of this type may be solved either by scale diagram or else by calculation,
(a) Graphical method: I think – after this illustration- you will be able to do it!.

(b) By calculation: If you did the graphical method, you can easily find out that
cos 50° × 20 N = horizontal component
so,
horizontal component = 20 × 0.6428 = 12.9
hence effective force = 12.9 N
Before leaving this problem it is of interest to consider the part played by the vertical force component. This acts against the weight of the roller, and therefore reduces the force which the roller exerts on the ground. On the other hand, if the roller is pushed instead of being pulled, the vertical component increases its effective weight.

To verify the triangle of forces

Triangle of forces experiment

A drawing board, pulleys, strings and weights is set up as described earlier and the positions of the strings marked out on paper.

We’ll, however, consider the results obtained from a different point of view. The three forces OE, OP and OQ are in equilibrium, that is so to say they exactly balance one another.
Any one of these forces is said to be the equilibrant of the other two.

If OR is made equal to OE we have already seen that OPQR is a parallelogram.

Now consider the triangle OPR.
Since PR is equal and parallel to OQ, it follows that PR will also represent n Newton in magnitude and direction, though not in position.
The sides of the triangle OPR therefore represent the three forces acting at O in magnitude and direction, but not necessarily in position. The experiment verifies the principle of the triangle of forces.

The triangle of forces principle:

If three forces acting at a point are in equilibrium, they can be represented in magnitude and direction by the three sides of a triangle taken in order.

Note. The expression “ taken in order” means that the arrows representing the force directions must follow one another in the same direction round the triangle.

Another worked example:

A 15 kg mass is supported by a thin cord attached to a hook in the ceiling. Another cord is attached to the ring of the mass and pulled horizontally until the supporting cord makes an angle of 30° with the vertical.
Find the tensions in both strings.
Solution
By trigonometry, 15 / T1 = cos 30°
therefore T1= 15 / cos 30° = 15/ 0.866 = 17.3 N
also,
T2/15 = tan 30°
therefore T2 = 15 tan 30° = 15 × 0.577 = 8.7 N.
Last note. The problem can also be solved by measurements from an accurate scale diagram.