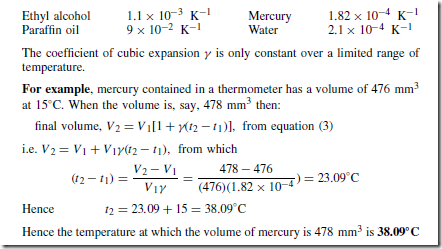When heat is applied to most materials, expansion occurs in all directions. Conversely, if heat energy is removed from a material (i.e. the material is cooled) contraction occurs in all directions. The effects of expansion and contraction each depend on the change of temperature of the material.
Some practical applications where expansion and contraction of solid materials must be allowed for include:
(i) Overhead electrical transmission lines are hung so that they are slack in summer, otherwise their contraction in winter may snap the conductors or bring down pylons.
(ii) Gaps need to be left in lengths of railway lines to prevent buckling in hot weather (except where these are continuously welded).
(iii) Ends of large bridges are often supported on rollers to allow them to expand and contract freely.
(iv) Fitting a metal collar to a shaft or a steel tyre to a wheel is often achieved by first heating them so that they expand, fitting them in position, and then cooling them so that the contraction holds them firmly in place; this is known as a ‘shrink-fit’. By a similar method hot rivets are used for joining metal sheets.
(v) The amount of expansion varies with different materials. Figure 30.1(a) shows a bimetallic strip at room temperature (i.e. two different strips of metal riveted together). When heated, brass expands more than steel, and since the two metals are riveted together the bimetallic strip is forced into an arc as shown in Figure 30.1(b). Such a movement can be arranged to make or break an electric circuit and bimetallic strips are used, in particular, in thermostats (which are temperature-operated switches) used to control central heating systems, cookers, refrigerators, toasters, irons, hot water and alarm systems.
(vi) Motor engines use the rapid expansion of heated gases to force a piston to move.
(vii) Designers must predict, and allow for, the expansion of steel pipes in a steam-raising plant so as to avoid damage and consequent danger to health.
Water is a liquid that at low temperature displays an unusual effect. If cooled, contraction occurs until, at about 4°C, the volume is at a minimum. As the
temperature is further decreased from 4°C to 0°C expansion occurs, i.e. the volume increases. When ice is formed, considerable expansion occurs and it is this expansion that often causes frozen water pipes to burst.
A practical application of the expansion of a liquid is with thermometers, where the expansion of a liquid, such as mercury or alcohol, is used to measure temperature.
The amount by which unit length of a material expands when the temperature is raised one degree is called the coefficient of linear expansion of the material and is represented by ˛ (Greek alpha).
The units of the coefficient of linear expansion are m/(mK), although it is usually quoted as just /K or KÐ1. For example, copper has a coefficient of linear expansion value of 17 ð 10Ð6 KÐ1, which means that a 1 m long bar of copper expands by 0.000017 m if its temperature is increased by 1 K (or 1°C). If a 6 m long bar of copper is subjected to a temperature rise of 25 K then the bar will expand by (6 ð 0.000017 ð 25) m, i.e. 0.00255 m or 2.55 mm. (Since the kelvin scale uses the same temperature interval as the Celsius scale, a change of temperature of, say, 50°C, is the same as a change of temperature of 50 K).
If a material, initially of length l1 and at a temperature of t1 and having a coefficient of linear expansion ˛, has its temperature increased to t2, then the new length l2 of the material is given by:
For example, the copper tubes in a boiler are 4.20 m long at a temperature of 20°C. Then, when surrounded only by feed water at 10°C, the final length of the tubes, l2, is given by:
Coefficient of Superficial Expansion
The amount by which unit area of a material increases when the temperature is raised by one degree is called the coefficient of superficial (i.e. area) expansion and is represented by ˇ (Greek beta).
If a material having an initial surface area A1 at temperature t1 and having a coefficient of superficial expansion ˇ, has its temperature increased to t2, then the new surface area A2 of the material is given by:
It may be shown that the coefficient of superficial expansion is twice the coefficient of linear expansion, i.e. ˇ D 2˛, to a very close approximation.
The amount by which unit volume of a material increases for a one degree rise of temperature is called the coefficient of cubic (or volumetric) expansion and is represented by y (Greek gamma).
If a material having an initial volume V1 at temperature t1 and having a coefficient of cubic expansion y, has its temperature raised to t2, then the new volume V2 of the material is given by:
It may be shown that the coefficient of cubic expansion is three times the coefficient of linear expansion, i.e. y D 3˛, to a very close approximation.
A liquid has no definite shape and only its cubic or volumetric expansion need be considered. Thus with expansions in liquids, equation (3) is used.
Some typical values for the coefficient of cubic expansion measured at 20°C
(i.e. 293 K) include:
