Electromagnetic waves

  When the wave theory of light first gained general acceptance it was considered that light waves were conveyed through a transparent elastic medium which filled the whole of space, even a vacuum. This substance was called the ether.

Michael Faraday's move

  A further step forward was made in 1845, when Michael Faraday showed that, under certain conditions, light was passing through a material medium were affected by a magnetic field.
Now by that time, it was known that there was an inseparable connection between magnetism and electricity. Faraday's experiment gave a strong hint that light might well have electrical properties
.

It is James Clerk Maxwell's move

  Some years later, the eminent mathematician and physicist, James Clerk Maxwell, became very interested in Faraday's work on electricity and eventually put forward a mathematical theory suggesting that an oscillating electric current should be capable of radiating energy in the form of electromagnetic waves (e.m. waves)..
An electromagnetic wave can be visualized as an oscillating electric force traveling through space accompanied by a similarly oscillating magnetic force in a plane at right angles to it.
  More importantly, Maxwell's equations led to the conclusion that such waves, if they existed, would travel with the same velocity as light ' C = 3 × 10⁸ m/s²'

Now, with Heinrich Hertz

The work of Heinrich Hertz

  Some twenty years after the publication of Maxwell's theory, the German scientist, Heinrich Hertz, showed that electromagnetic waves could indeed be produced by means of an oscillating electric spark. Moreover, he performed numerous experiments to demonstrate that the newly discovered waves underwent reflection, refraction, diffraction and interference: In short,
they behave exactly like light waves but a much greater wavelength.
  The inference was that light waves themselves were also electromagnetic and further experimental and theoretical studies have since confirmed this belief.

  The work of Hertz was developed by Marconi and others who laid the foundations of our present-day use of electromagnetic waves in radio communication.

  The image shows the whole range of electromagnetic waves in order of increasing wavelengths. Any particular range of wavelengths is referred to as a band. You'll notice that the visible wavelengths occupy a very small band in the complete electromagnetic spectrum.

The SI unit of frequency

  In recognition of the importance of Hertz's researches into electromagnetic waves, his name has been given to the unit of frequency.

  The SI unit of frequency is called the hertz (Hz) and is equal to a frequency of 1 cycle per second (formerly written as 1 c /s).
  The term hertz is not restricted to wave frequencies only but is used for any regularly event, e.g., the frequency of a pendulum, on alternating current, a musical note and so on.
  Larger frequency units in common use are
    the kilohertz (kHz) = 1000 Hz

    the megahertz (MHz) = 1000000 or 10⁶ Hz

    the gigahertz (GHz) = 10⁹ Hz
.
  Example.
Calculate the frequency of a radio wave of wavelength 150 meter..
  The The velocity of all e.m. waves in free space = 3 × 10⁸ m/s².
For a wave,

v = frequency × wavelength = f λ

hence, f = v/λ =3 × 10⁸/150 = 2 × 10⁶ Hz
 

The inverse square law for electromagnetic waves

wave intensity
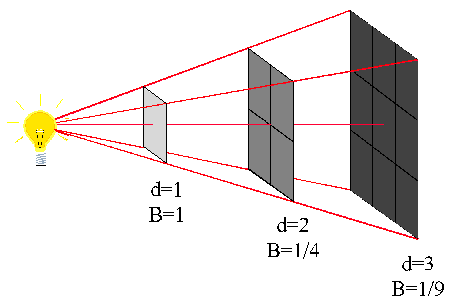
  Let us suppose that an area of 1 m² which forms part of the surface of a sphere of radius 1m receives wave energy from a point source placed at the center.
  If P is the energy passing through this unit area in joules per second, i.e, if P is the power in watts, then we say that P is the wave intensity in W/m².
  If the distance is increased to 2 m it is clear from geometry of the figure "at your right" that the same power is now spread over an area of 2² = 4 m². Consequently the wave intensity is reduced to P/4.
  Similarly, when the distance is increased to 3 m the wave intensity in W/m² is now only P/9.
 

Wave intensity is defined as the power transmitted per unit area of the wavefront

  In general, the wave intensity at any distance x from a point source is given by the equation:
  The relation between wave intensity and distance is expressed by the inverse square law, which states that,

The electromagnetic wave intensity from a point source in free space is inversely proportional to the square of the distance from the source.

 

Light as a special case

The measurement of light wave energy 'photometry' is complicated by the fact that light sources contain non-visible radiation as well, e.g., ultraviolet and infrared. Special units called Lux (not W/m²) therefore have to be used, but all the same,the inverse square law STILL HOLDS.

Attenuation

  The inverse square law for radiation as represented above holds strictly for waves through free space from a point source. If the radiation passes through a material medium of some kind then the law is modified by the fact that some of wave energy is progressively absorbed.

The loss of power from this cause is described as attenuation.

Origin and sources of electromagnetic waves

  The whole range of electromagnetic radiation pours on to the earth from the sun and other heavenly bodies in outer space. Those frequencies which are stopped by the earth's atmosphere have been detected by instruments in man-made satellites orbiting the earth.
  Otherwise some of the main sources on earth are given in the table below.

Wave-Band	Origin	Sources
X-radiation	1- High energy changes in electron structure of atoms. 2- Decelerated electrons	X-ray tubes
Gamma radiation	Energy changes in nuclei of atoms	Radioactive substances
Ultraviolet Radiation	Fairly high energy changes in electron structure of atoms	1- Very hot bodies, e.g., the electric arc. 2- Electric discharge through gases, particularly mercury vapor in quartz envelopes.
Visible Radiation	Energy changes in electron structure of atoms	Various lamps, flames and anything at or above red-heat.
Infrared Radiation	Low energy changes in electron structure of atoms	All matter over a wide range of temperature from absolute zero upwards
Radio Waves	1- High-frequency oscillatory electric currents 2- Very low energy changes in electron structure of atoms	Radio transmitting circuits and aerial equipment