This is a quote I like very much:
“Great minds have purposes, others have wishes.”
Washington Irving
Now let’s have a purpose, learning :)
Every time we open a door, turn on a tap or tighten up a nut with a spanner, we exert a turning force.
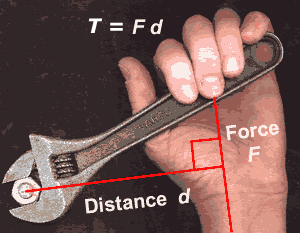
Two factors are involved here,
1- The magnitude of of the force applied
2- The distance of its line of action from the axis or fulcrum about which turning takes place.
A very large turning effect can be produced with a comparatively small force provided the distance from the fulcrum is large. For this reason, it is easier to loosen a tight nut with a long spanner than with a short one.
Experienced mechanics are aware that long spanners must be used with care, as it is easy to strip screw threads by too large a turning force.
I think you –my dear reader- are ready for the following definition.
The moment of the force
The combined effect of the force and distance which determines the magnitude of the turning force is called the moment of the force and is defined as follows.
The moment of a force about a point is the product of the force and the perpendicular distance of its line of action from the point.
Two experiments to study moments
Experiment (1).
A small hole is drilled in a meter rule on the 50 cm mark but slightly offset from the centre.
The rule is then pivoted on a knitting needle so that it balances horizontally.
Now, if one side of the rule happens to be slightly heavier it will tilt, but this can be corrected by means of U-shaped rider made of thick copper wire. The rider is placed on the lighter side of the rule and its position adjusted until the rule becomes horizontal.
Unequal weights, W1 and W2 are now hung from cotton loops on either side of the rule and their distances, d1 and d2, from the pivot are adjusted until rule once more comes to rest horizontally. The weights are now exerting equal and opposite moments about the pivot.
The experiment is repeated a number of times using different pairs of weights and distances and the results tabulated.
Making allowance for experimental error, it will be seen that in every case the product,
force × distance on the left hand side is equal to the product,
force × distance on the right hand side.
We therefore conclude that the product, force × distance from the fulcrum measures the turning effect of the force.
Experiment (2). (I’m sorry, the image is not available. Use your imagination please)
In the previous experiment the string supporting the weights were at right angles to the rule, and therefore the distance along the rule was also the perpendicular distance from the fulcrum.
In the second experiment the same apparatus is used, except that one of the strings is passed over a pulley, so that the line of action of the force W1 is not now at right angles to the rule.
The rule is balanced horizontally as before by suitably adjusting the positions of the strings along it. The perpendicular distance of the line of action of W1 from F is now equal to FB. This distance, d1 , is measured with a half-meter rule and is entered in a table together with W1 , W2 and d2 .
When the products W1 d1 and W2 d2 are worked out they are once more found to be equal.
This shows that the turning effect of W1 in this experiment is given by
W1 × FB and not W1 × FA.
These experiments verify the principle of moments
Principle of moments
When a body is in equilibrium, the sum of the anticlockwise moments about any point is equal to the sum of the clockwise moments.
Resultant moment problem
When dealing with problems involving a number of moments acting on a body which is not in equilibrium, the first step is to draw a sketch indicating the forces and their distances from a fulcrum.
It is customary to give a positive sign to anticlockwise moments and negative sign to clockwise moments.
The various moments are written down with appropriate signs and are added algebraically.
The sign of the answer will then give the direction of the resultant moment.
Let’s see an example..
A rod AE of negligible weight, 40 cm long, is pivoted at a point D. Weights of 10, 20, 30 and 40 Newton act on the rod as shown in the image.
Taking the forces acting from left to right, we have
Sum of moments = (10 × 30) - (30 × 20) + (20 × 10) - (40 × 10) = – 500 Newton.meter.
Hence the resultant moment is 500 Newton.meter units acting in clockwise direction.
Parallel forces. Couples
Parallel force which act in the same direction are called like forces, and it is always possible to find their resultant or the single force which exactly replace them.
The same usually applies in the case of parallel forces which are unlike or act in opposite directions. There is, however, one special case in which a single resultant force cannot be found, namely, where the forces can be shown to be equivalent to two equal and opposite parallel forces.
Equal and opposite parallel forces form what is called a couple.
It is not possible to find a single force to replace a couple. A couple simply produces rotation and can only be balanced by an equal and opposite couple.
To study parallel forces in equilibrium
A meter rule is weighed and then suspended by vertical threads attached to two spring balanced held by clamp and stand.
Two weights are attached so that one exerts an upward and the other a downward pull on the rule.
Lastly, the spring balances are raised or lowered as necessary to bring the rule into a horizontal position.
We shall assume, for the time being, that the force of gravity on the rule itself acts downwards through its centre. In this case the centre of the rule is also its centre of gravity “mass”, and this will be explained more fully in the next post.
It will be noted that
The sum of the upward forces = The sum of the downward forces
Furthermore, as the rule is in equilibrium, there is no resultant moment acting which would cause it to turn about any point.
This may be verified by working out the moments of the forces about any point we choose and showing that the sum of the anticlockwise moments is equal to the sum of the clockwise moments.
It is convenient to do this by entering the various forces and distances in a table. In accordance with convention, anticlockwise moments are given a positive sign and clockwise moments a negative sign. See the table below as an example..
Summary
When a number of parallel forces are in equilibrium:
1- The sum of the forces in one direction is equal to the sum of the forces in the opposite direction;
2- The sum of the anticlockwise moments about any point is equal to the sum of the clockwise moments about the point.
When performing this experiment, you should use different weights and distances and draw an appropriate diagram. The results should be entered in a table and a different point chosen about which moments are taken.
| Force (in Newton) | Distance (in meter) | Moment about a point (in Newton.meter) |
| 105 ‘anticlockwise’ | 10 | + 1050 |
| 20 ‘anticlockwise’ | 20 | + 400 |
| 220 ‘clockwise’ | 50 | - 11000 |
| 50 ‘clockwise’ | 70 | – 3500 |
| 145 ‘anticlockwise’ | 90 | + 13050 |
| Sum of anticlockwise moments | (+) 14500 Newton.meter | |
| Sum of clockwise moments | (-) 14500 Newton.meter |